Schrittgetriebe
Schrittgetriebe setzen eine kontinuierliche Drehbewegung in eine schrittweise Bewegung um. Zwischen den Schritten (den Schaltphasen) steht der Getriebeausgang still, bis der nächste Schritt beginnt. In der Regel ist auch die Bewegung am Getriebeausgang eine Drehbewegung. Die Bewegung am Getriebeausgang geht immer in die gleiche Richtung. Schrittgetriebe sind mit fast allen Getriebearten umsetzbar.
Spezielle Formen von Schrittgetrieben erzeugen Pilgerschritt-Bewegungen. Die Bewegung am Getriebeausgang läuft dabei nicht konsequent in die gleiche Richtung, sondern enthält kleine oder auch größere Rückwärtsbewegungen.
Beispiele dafür sind die Drehbewegungen in einem kurvengesteuerten Werkzeugwechsler oder die Herstellung von Rohren im Pilgerschrittverfahren.
Getriebe, die normalerweise für die Erzeugung von Schrittbewegungen verwendet werden, können auch so modifiziert bzw. ausgelegt werden, dass am Abtrieb ganz allgemeine durchlaufende Bewegungen ohne Rasten entstehen. Das erweitert die Anwendungsmöglichkeiten der Schrittgetriebe enorm. Man kann dann zwar nicht mehr von "Schritten" reden, der Schrittgetriebe-Charakter der Kinematik bleibt aber erhalten.
Von besonderer Bedeutung für die Praxis sind die Kurven-Schrittgetriebe, speziell die Parallelkurvengetriebe (auch ebene Rollensterngetriebe oder CF3-Getriebe genannt), die Zylinderkurven-Schrittgetriebe und die Globoidkurven-Schrittgetriebe, auch Servoantriebe zur Erzeugung von Schrittbewegungen.
Darüber hinaus gibt es eine Reihe anderer Bauformen, beispielsweise mit mehreren Antrieben, nur aus Rädern bestehend, als reine Koppelgetriebe und noch noch noch speziellere Formen, die man in der Praxis nur selten antrifft. Ingenieure sind sehr erfindungsreich!
Wir befassen uns als Spezialist für Kinematik und Kurvenberechnungen seit Jahrzehnten mit allen Formen von Schrittgetrieben und unterstützen Sie gern bei Ihren Anwendungen!
Direkt zu ...
- Begriffe
- Berechnung
- Kurven-Schrittgetriebe
- Globoidkurven-Schrittgetriebe
- Zylinderkurven-Schrittgetriebe
- Parallelkurven-Schrittgetriebe
- Servogesteuerte Schrittbewegungen
- Malteserkreuzgetriebe
- Sternradgetriebe
- Kurvenscheibe mit umlaufendem Hebel
- Räderkoppelgetriebe
Zur Startseite von Nolte NC-Kurventechnik GmbH
> English version of this page
Begriffe
Speziell bei den besonders verbreiteten Kurven-Schrittgetrieben sind einige Fachbegriffe bedeutsam. Die Wissenschaft möge mir nachsehen, dass ich bei Winkeln hier in Grad rechne.
Achsabstand
Die wichtigste Hauptabmessung im Getriebe aus Sicht des Anwenders und des Herstellers: der kinematische Abstand zwischen Antriebsachse und Abtriebsachse, also Getriebeeingang und Getriebeausgang. Kataloge der Schrittgetriebehersteller sind in der Regel nach dem Achsabstand gestaffelt, die maßgeblich die Baugröße bestimmt. Weitere kinematische Abmessungen, wie z.B. der Rollendurchmesser, der Rollen-Teilkreisdurchmesser oder der Kurven-Außendurchmesser, sind zwar auch von großer Bedeutung, aber eigentlich nur für Auslegung und Berechnung und damit für den Hersteller.
Ebenenanzahl
Bei Parallelkurvengetrieben (CF3-Getrieben / Ebenen Rollensterngetrieben) ist die Ebenenanzahl die Anzahl der Kurvenscheiben am Antriebsglied und damit auch die Anzahl der Rollenebenen am Abtriebsglied. Parallelgetriebe haben meist zwei Ebenen, es gibt aber auch Bauformen mit drei, theoretisch auch noch mehr Ebenen.
Teilungswinkel
Im Regelfall sind die Rollen auf dem Rollenstern (dem Kurven-Abtriebsglied) auf einem Teilkreisdurchmesser gleichmäßig verteilt. Der geometrische Winkel zwischen zwei Rollen ist dann der Teilungswinkel.
Teilungswinkel = 360 Grad / Rollenzahl
Stationenzahl / Stoppzahl
Die Stationenzahl legt fest, nach wievielen Schritten der Getriebeausgang eine Umdrehung vollendet. Sie wird auch Stoppzahl genannt.
Schrittzahl
Die Schrittzahl, in der Praxis auch Teilung genannt, ist die Anzahl der Schritte am Getriebeausgang während einer Umdrehung am Getriebeeingang
Doppelschaltung / N-fach-Schaltung
Bei einer Doppelschaltung erfolgen bei jeder vollen Umdrehung der Antriebswelle zwei Schaltungen. Die Schrittzahl ist dann 2.
Bei einer N-fach-Schaltung erfolgen bei jeder vollen Umdrehung der Antriebswelle N Schaltungen. Die Schrittzahl ist dann N.
Schrittwinkel
Der Schrittwinkel ist der Winkel, den der Getriebeausgang zwischen Anfang und Ende einer einzelnen Schaltung durchläuft.
Schrittwinkel = 360 Grad / Stationenzahl
Genauer ist der Schrittwinkel der Differenzwinkel zweier aufeinanderfolgender Rasten am Getriebeausgang. Bei angenäherten Rasten bezieht man sich auf die mittleren Rastlage.
Der Schrittwinkel ist ein ganzzahliges Vielfaches des Teilungswinkels. Bei Parallelgetrieben ist der Schrittwinkel auch ein ganzzahliges Vielfaches von Teilungswinkel•Ebenenzahl
Schaltwinkel
Der Schaltwinkel ist der Drehwinkel am Getriebeeingang während einer Schaltphase. Bei angenäherten Rasten bezieht man sich auf das Verlassen bzw. das Erreichen der mittleren Rastlage.
Rastwinkel
Der Rastwinkel ist der Drehwinkel am Getriebeeingang während einer Rastphase. Er kann auch 0 sein. Dann hält der Getriebeausgang nur in einem Moment an.
Periodenwinkel
Der Periodenwinkel ist der kleinste Antriebswinkelbereich, nach dem sich die Bewegungen am Getriebeausgang wiederholen. Der Periodenwinkel muss nicht 360 Grad sein.
Periodenwinkel = 360 Grad / Schrittzahl
Rastwinkel + Schaltwinkel = Periodenwinkel
Drehzahl
Normalerweise nimmt man bei der Auslegung eines Schrittgetriebes an, dass die Eingangswelle mit konstanter Winkelgeschwindigkeit bzw. Drehzahl in U/min läuft.
Taktzahl
Die Taktzahl ist die Anzahl Schalt-/Rastzyklen pro Minute.
Taktzahl = Drehzahl•Schrittzahl
Wenn die Taktzahl im Kurvenberechnungsprogramm sich jedoch auf den kompletten Berechnungszyklus bezieht, dann ist
Taktzahl = Drehzahl
Taktzeit / Zykluszeit
Die Taktzeit, auch Zykluszeit genannt, ist die Zeit für einen Schalt-/Rast-Zyklus.
Taktzeit in s = 60 s/min / (Taktzahl in 1/min)
Taktzeit = Schaltzeit + Rastzeit
Schaltzeit
Die Schaltzeit ist Zeit für eine einzelne Schaltphase.
Rastzeit
Die Rastzeit ist die Zeit für eine Rastphase.
Rastabweichung
Bei Schrittgetrieben mit angenäherter Rastphase ist die Rastabweichung die Schwankungsbreite der Abtriebslagen um die mittlere Rastlage.
Bezogene Rastabweichung
Bei Schrittgetrieben mit angenäherter Rastphase ist die bezogene Rastabweichung die Schwankungsbreite der Abtriebslagen um die mittlere Rastlage, bezogen auf den Schrittwinkel der vorausgegangenen Schaltphase. Die bezogene Rastabweichung ist also ein relativer Fehler und damit ein Maß für die Güte der Rast.
Rast-Perioden-Verhältnis
Das Rast-Perioden-Verhältnis ist der auf den Antriebswinkel bezogene Anteil der Rast an einer Periode.
Rast-Perioden-Verhältnis = Rastwinkel/Periodenwinkel = Rastwinkel/(Rastwinkel+Schaltwinkel)
Wenn die Bewegungsperiode mehrere Rasten enthält, rechnet man alle Rastwinkel in der Bewegungsperiode zusammen:
Rast-Perioden-Verhältnis = (Summe aller Rastwinkel)/Periodenwinkel
Schalt-Perioden-Verhältnis
Das Schalt-Perioden-Verhältnis ist der auf den Antriebswinkel bezogene Anteil der Schaltung an einer Periode.
Schalt-Perioden-Verhältnis = Schaltwinkel/Periodenwinkel = Schaltwinkel/(Rastwinkel+Schaltwinkel)
Wenn die Bewegungsperiode mehrere Rasten enthält, rechnet man alle Schaltwinkel in der Bewegungsperiode zusammen:
Schalt-Perioden-Verhältnis = (Summe aller Schaltwinkel)/Periodenwinkel
Rast-Perioden-Verhältnis + Schalt-Perioden-Verhältnis = 1
Gängigkeit
Bei räumlichen Kurven-Schrittgetrieben (Zylinderkurven- und Globoidkurven-Schrittgetrieben) ist die Gängigkeit die Anzahl Kurvennuten bzw. "Gänge", die für die Bewegungsübertragung benötigt werden.
Gängigkeit = Schrittwinkel / Teilungswinkel
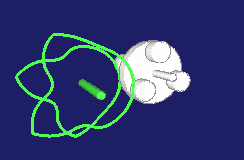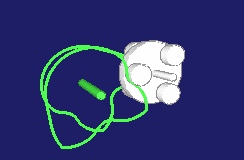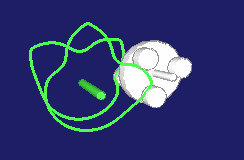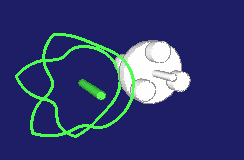
Die Animation zeigt links ein eingängiges Globoidkurven-Schrittgetriebe, in der Mitte ein zweigängiges und rechts ein dreigängiges:
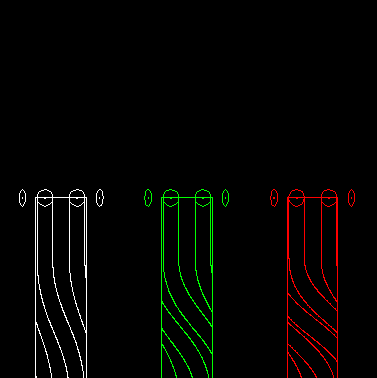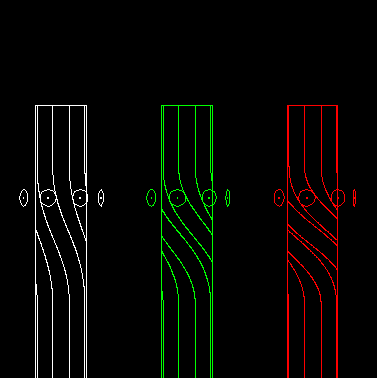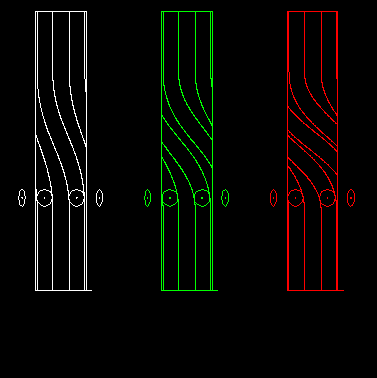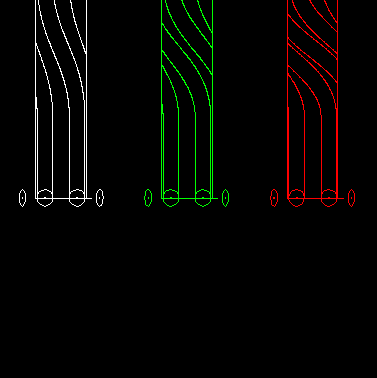
Das läßt sich auch auf Parallelgetriebe übertragen.
Wenn n (mindestens 4) Rollen an der Bewegungsübertragung eines Schrittes beteiligt sind, ist
Gängigkeit = n / Ebenenzahl - 1
Bei Parallelgetrieben entstehen Schnittpunkte zwischen den Kurvenprofilen, die für die einzelnen Rollen berechnet werden können. Die Anzahl Schnittpunkte m bei einer einzelnen Kurvenscheibe ist
m = Ebenenzahl•Gängigkeit
MS, MS30, MS50, P5, TR, MT
Dies sind praxisübliche Bezeichnungen für die bekanntesten Bewegungsgesetze, die in Kurven-Schrittgetrieben verwendet werden:
MS = Modifizierte Sinuslinie (Modifizierte Sinuide, Modified Sine)
MS30 = Modifizierte Sinuslinie mit 30% Geradeneinschub
MS50 = Modifizierte Sinuslinie mit 50% Geradeneinschub
P5 = Polynom 5. Grades (Polynomial 5th degree)
MT = TR = Modifiziertes Beschleunigungstrapez (Modified Trapezoidal)
Jeder Getriebehersteller kann sein eigenes Bezeichnungssystem haben, und es gibt natürlich noch sehr viel mehr Bewegungsgesetze..
Viele dieser Begriffe werden in der VDI-Richtlinie 2727, Blatt 3, behandelt, die sich speziell mit den Schrittgetrieben befasst.
Kurven-Schrittgetriebe
Schrittgetriebe auf Basis von
sind besonders leistungsfähig und flexibel und deshalb sehr verbreitet.
Jeder dieser drei Getriebebauformen haben wir deshalb eine eigene Seite spendiert. Bitte klicken Sie auf die Menüpunkte!
Weltweit setzen etliche renommierte Hersteller von Kurven-Schrittgetrieben auf unsere Software OPTIMUS MOTUS!
Parallelkurven-Schrittgetriebe:
Globoidkurven-Schrittgetriebe:
Zylinderkurven-Schrittgetriebe:
Servogesteuerte Schrittbewegungen
Eine auch in der Praxis oft verwendete Möglichkeit, Schrittbewegungen oder generell durchlaufende Bewegungen zu erzeugen, sind Servoantriebe.
Malteserkreuzgetriebe
Ein Klassiker unter den Schrittgetrieben ist das Malteserkreuzgetriebe, bei dem Antriebs- und Abtriebswelle parallel sind.
Ein umlaufend angetriebener Bolzen greift in eine der Nuten der Abtriebsscheibe ein und bewegt sie um eine Teilung weiter. Außerhalb dieser Schaltphase, wenn der Bolzen also nicht in eine Nut eingreift, fixiert eine Arretierung die Abtriebsscheibe. Wenn mehrere Bolzen auf der Antriebsscheibe angebracht werden, eventuell sogar ungleichmäßig verteilt, sind vielfältige Schaltrhythmen denkbar.
Da der Bolzen tangential in die geraden Nuten einlaufen muss, ergibt sich der Schaltwinkel direkt aus dem Schrittwinkel, kann den Schaltwinkel bzw. die Aufteilung Rastzeit zu Schaltzeit also nicht frei gestalten.
Bei einem Schrittwinkel von 90 Grad, bei dem sich auch ein Schaltwinkel von 90 Grad ergibt, erinnern die vier Nuten zusammen mit der kreisförmigen Aussparung auf der Abtriebsscheibe für die Arretierung an ein Kreuz des Malteser-Ordens. So kommt der Name zustande.
Das klassische Malteserkreuzgetriebe ist ruckbehaftet, d.h. bei gleichmäßigem Antrieb treten Beschleunigungssprünge am Getriebeausgang auf.
Die Animation zeigt eine Schaltung des Malteserkreuz-Schrittgetriebes, und unten ist in rot der Beschleunigungsverlauf am Getriebeausgang dargestellt. Neben dem Ruck (= Beschleunigungssprung) ist auch der Verlauf der Beschleunigung nicht optimal.
Für höhere dynamische Anforderungen ist das Malteserkreuzgetriebe deshalb nicht geeignet.
Weil das Abtriebsrad eines Malteserkreuzgetriebes aussieht wie ein Stern, wird es oft auch "Sternrad" genannt. Ein Sternradgetriebe funktioniert aber ganz anders als ein Malteserkreuzgetriebe.
Das Malteserkreuzgetriebe kann mit Hilfe eines Zykloidengetriebes auf der Antriebsseite so modifiziert werden, dass am Getriebeausgang ein sehr harmonischer Bewegungsablauf ohne Ruck entsteht. Die zweite Animation zeigt ein solches Getriebe inklusive Beschleunigungsdiagramm. Die Maximalwerte der Beschleunigung sind aber sehr hoch, erheblich höher als die Beschleunigungen, die man mit Kurven-Schrittgetrieben erreicht.
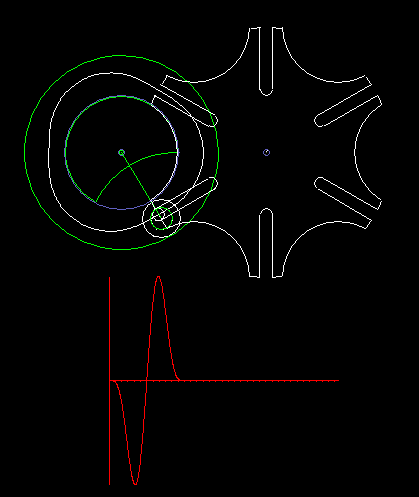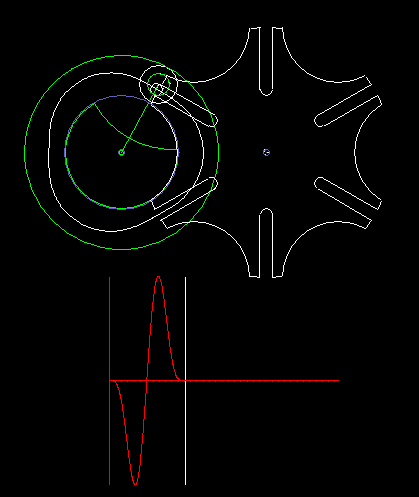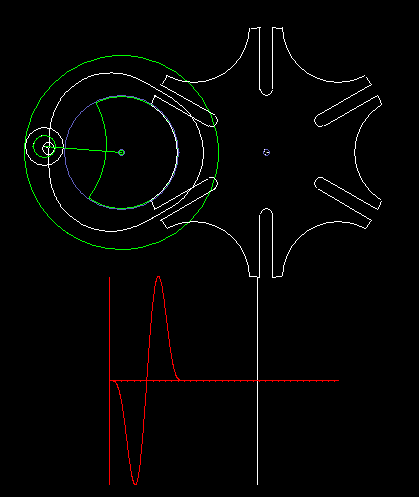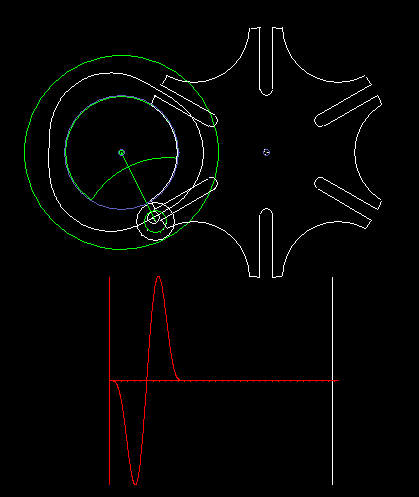
Statt des Zykloidengetriebes können alle Mechanismen vorgeschaltet werden, die den Bolzen auf ihrer Koppelkurve tangential und mit Krümmung 0 in die Nuten auf der Abtriebsscheibe einführen. Mit Viergelenkgetrieben ergeben sich jedoch keine attraktiven Lösungen in Bezug auf die Beschleunigungen am Getriebeausgang, und höhergliedrige Koppelgetriebe machen die Kinematik sehr aufwändig.
Sternradgetriebe
Sternradgetriebe (nicht "Stirnradgetriebe"!) sind Schrittgetriebe auf Basis von Rädergetrieben. Dieses Basisgetriebe kann mit Stirnrad- oder Triebstockverzahnungen ausgeführt sein.

Von der Idee her wird die Übertragung der Drehbewegung von Antriebsrad auf Abtriebsrad ausgesetzt, indem man auf dem Abtriebsrad einige Zähne auslässt. Kurvensegmente sorgen für einen relativ weichen Übergang zwischen konstanter Winkelgeschwindigkeit im Mittelteil der Schaltphase und der Rast.
Eine Arretierung sorgt dafür, dass das Abtriebsrad während der Rastphase fixiert ist.
Antriebs- und Abtriebswelle sind parallel zueinander.
Gegenüber dem Malteserkreuzgetriebe können Schrittzahl, Schrittwinkel und Rastwinkel erheblich breiter variiert werden. Außerdem müssen die Schrittwinkel in einer Periode nicht gleich sein. Da die Schaltphase hauptsächlich mit einer konstanten Geschwindigkeit durchlaufen wird und nur ein geringer Antriebswinkel für den Übergang aus oder in die Rast übrig bleibt, werden am Abtriebsrad sehr große Winkelbeschleunigungen auftreten.
Mit Sternradgetrieben können sowohl Übersetzungen als auch Untersetzungen erzeugt werden. Es ist variabler einsetzbar als das Malteserkreuzgetriebe, aber auch aufwändiger und teurer.
Sternradgetriebe werden manchmal fälschlicherweise für Planetengetriebe gehalten.
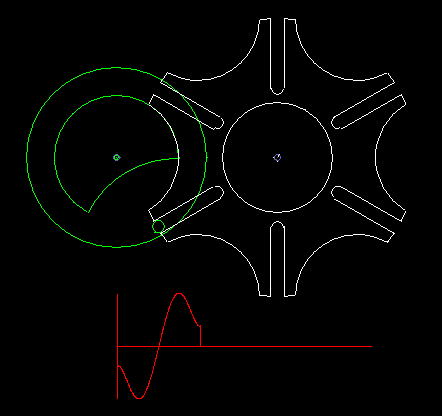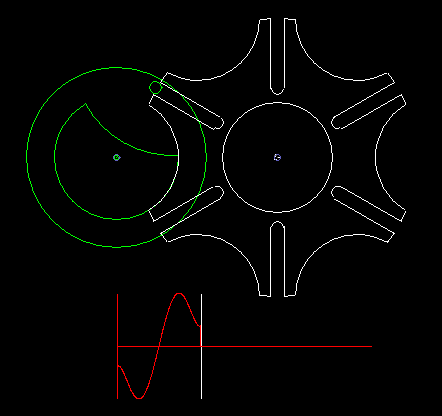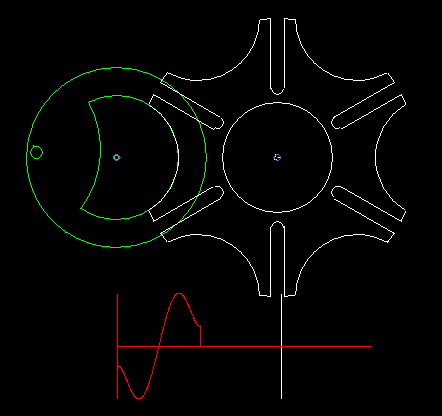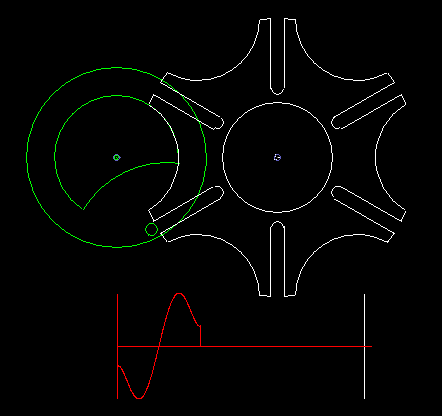
Kurvenscheibe mit umlaufendem Hebel
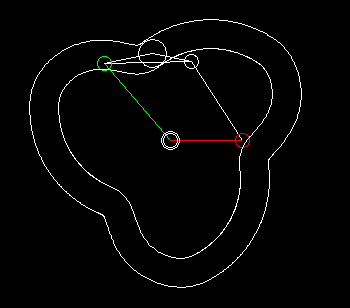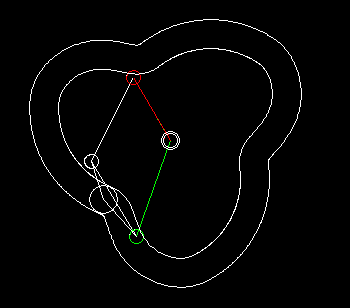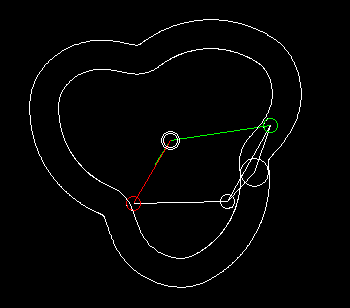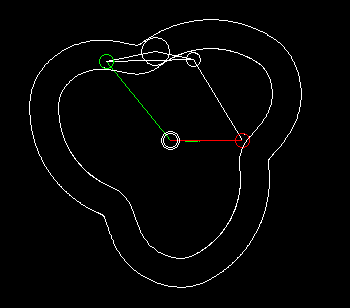
Eine einfache Form eines kurvengesteuerten Schrittgetriebes zeigen die beiden folgenden Animationen.
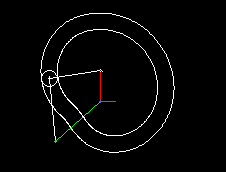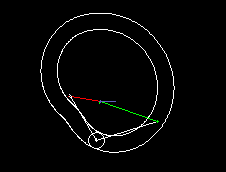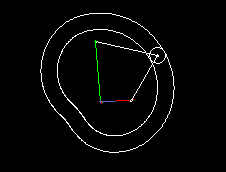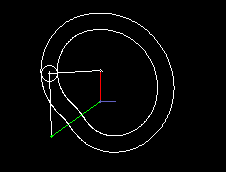
Die erste zeigt eine Einfachschaltung, die zweite eine Dreifachschaltung.
Grün ist der gleichmäßig umlaufende Antrieb dargestellt, rot der schrittweise bewegte Abtrieb. Über den Kurvenhebel und eine Koppel (beide weiß dargestellt) wird das Abtriebsglied gegenüber dem Antrieb so verzögert bzw. beschleunigt, dass phasenweise Rasten am Getriebeausgang entstehen.
Eingangs- und Ausgangswelle liegen parallel und eng beieinander, meistens sogar in einer Flucht. Bei der Bewegungsgestaltung hat man zwar nicht so viele Freiheiten wie bei Parallelgetrieben, Zylinderkurven-Schrittgetrieben oder Globoidkurven-Schrittgetrieben, denn es entstehen schnell Mechanismen mit sehr schlechtem Übertragungswinkel, trotzdem kann die Übertragungsfunktion ruckfrei gestaltet werden.
Statt einer Nutkurve können auch Steg- oder Doppelkurven verwendet werden.
Räderkoppelgetriebe
Schrittgetriebe mit angenäherter Rast können in Form von Räderkoppelgetrieben umgesetzt werden.
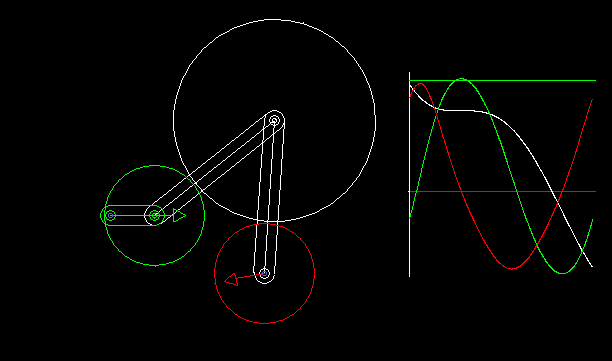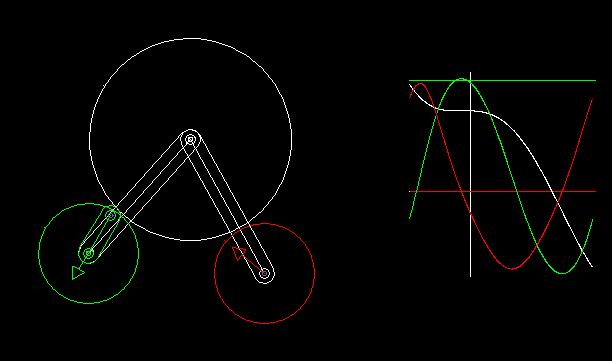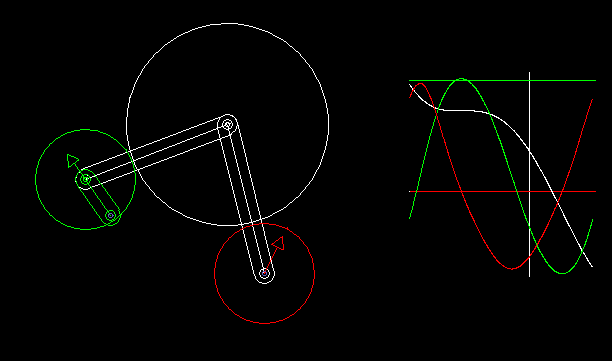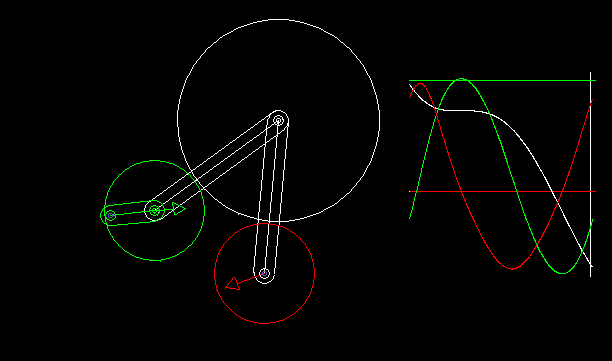
Mit den Getriebesynthese-Funktionen der Software OPTIMUS MOTUS können wir die kinematischen Abmessungen der Getriebe für die bestmögliche Einhaltung gewünschter Rastwinkel numerisch optimieren.
Die Animation zeigt ein Räderkoppelgetriebe und die Verläufe von Weg (weiß), Geschwindigkeit (grün) und Beschleunigung (rot) der Drehung der Ausgangswelle.
Längere Phasen angenäherter Rast erfordern komplexere Koppelgetriebe. Das macht die Konstruktion unattraktiv.
Zur Startseite von Nolte NC-Kurventechnik GmbH
Start Fachberichte Mechanismen Kinematik Kurvengetriebe Servo/SPS Bewegungsdesign Fortbildung Software Service Kurvenberechnung Impressum Datenschutz
Begriffe Kurvenschrittgetriebe Globoidkurvenschrittgetriebe Zylinderkurvenschrittgetriebe Parallelkurvenschrittgetriebe Malteserkreuz Sternradgetriebe Nutkurvenschrittgetriebe Räderkoppelschrittgetriebe
11/06/21
• Software OPTIMUS MOTUS ® /
DasNolte ®
• Berechnung von Kurven aller Art
• Performance-Optimierung
• Trainings und Beratung
• App- und Software-Entwicklung
• SPS-Bewegungsprogramme
Kurven, Mechanismen, Bewegungsdesign. Für schnellere Maschinen. Seit 1965.