Getriebesynthese
Die Synthese von Koppelgetrieben (auch Gelenkgetriebe genannt) ist auch über 100 Jahre nach Burmester immer noch ein kniffliges Gebiet für Mechanismentechniker.
Das Ziel bei der Getriebesynthese besteht immer darin, einen Mechanismus mit gewünschten Führungseigenschaften, Übertragungseigenschaften oder energetischen Eigenschaften zu finden.
Beispielsweise soll er eine bestimmte Koppelkurve oder eine vorgegebene Übertragungsfunktion erzeugen.
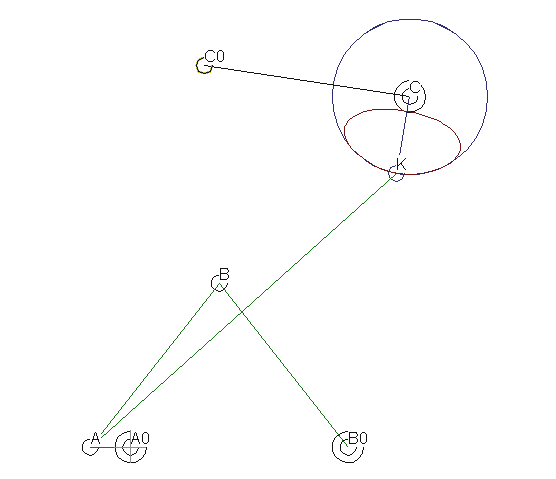
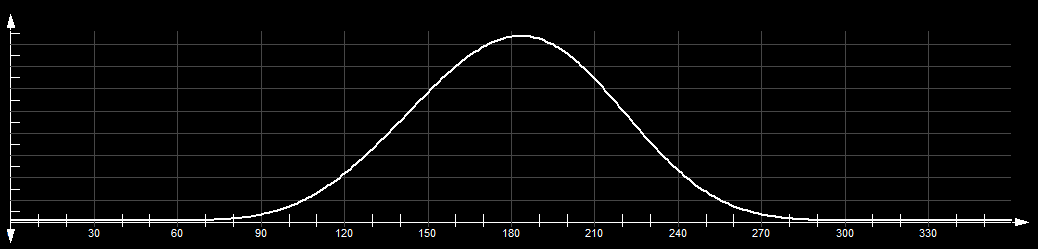
Im Bild ist ein sechsgliedriges Koppelgetriebe dargestellt, das an der Abtriebsschwinge C0-C eine relativ lange und relativ genaue Rastposition einhält, wenn man die Kurbel A0-A um 360 Grad dreht. Hier die Übertragungsfunktion des Koppelrastgetriebes:
Die Synthese-Aufgabe wird einfacher, wenn man die Verwendung von Kurvengelenken erlaubt, denn dann kann man meist relativ schnell eine geeignete Getriebestruktur festlegen und die Kurvenbahnen direkt ausrechnen, mit denen der Mechanismus die vorgegebenen Eigenschaften hat.
Wir verstehen unter Koppelgetriebesynthese die speziellere Aufgabe, Mechanismen nur mit Drehgelenken und Schubgelenken zu finden, um die Bewegungsaufgabe umzusetzen.
Allerdings fällt die Suche nach Mechanismen mit Rädern und Zugmitteln in die gleiche Aufgabenkategorie, weil die Lösungsmethoden ähnlich sind.
Der wesentliche Punkt ist, auf frei gestaltbare Kurven zu verzichten.
Das macht die Getriebesynthese so schwierig, denn dann hat man nur endlich viele Parameter, um die Übertragungsfunktion, die Koppelkurven, die Antriebsmomentenverläufe und die Gelenkkraftverläufe zu optimieren. Die Vorgaben sind so in aller Regel nur näherungsweise erfüllbar. Man sucht den Mechanismus, mit dem man die Forderungen bestmöglich umsetzen kann, und hofft, dass die Abweichungen von der Vorgabe noch akzeptabel sind.
Dieser Aufwand kann sich aber lohnen:
Mechanismen, die nur Drehgelenke enthalten, sind besonders einfach herzustellen, von Natur aus verschleißarm und harmonisch in ihren Bewegungen.
Wenn man besonders hohe Taktzahlen erreichen oder den Verschleiß reduzieren will, sollte man versuchen, Mechanismen nur mit Drehgelenken zu finden, die die vorgegebene Bewegungsaufgabe mit definierter Toleranz erfüllen.
Es ist oft durchaus möglich, Kurven oder Linearführungen durch Lösungen mit Drehgelenken zu ersetzen!
Wir vertreten mit unseren Dienstleistungen und unserer Software OPTIMUS MOTUS einen numerischen Ansatz, mit dem man vom Grundsatz her Lösungen für beliebige Getriebesynthese-Aufgaben finden kann. Dabei berücksichtigen wir nicht nur kinematische Vorgaben, sondern auch kinetostatische und energetische.
Direkt zu ...
- Struktursynthese
- Zeichnerische Maßsynthese
- Numerische Maßsynthese
- Newton-Verfahren
- Festlegen geeigneter Optimierungsparameter
- Zielfunktion
- Einflussgrößenberechnung
- Suchfeldberechnung
- Suchschrittoptimierung
- Zusammengesetzte Optimierungen
- Beispiel Geradführungsmechanismus
- Software
- Berechnung
zur Startseite von Nolte NC-Kurventechnik GmbH
> English version of this page
Struktursynthese
Die Synthese eines Mechanismus für eine Bewegungsaufgabe beginnt damit, eine geeignete Getriebestruktur zu finden und für die anschließende Maßsynthese festzulegen. Typische Bewegungsaufgaben sind Bewegungsübertragungen, Punktführungen oder Ebenenführungen.
- Je einfacher die Mechanismenstruktur, desto besser.
- Wenige bewegte Teile sind besser als viele bewegte Teile.
- Drehgelenke sind besser als Schubgelenke oder Kurvengelenke.
Als erster Kandidat für sehr viele Syntheseaufgaben kommt das Viergelenkgetriebe in Frage. Das Koppelrastgetriebe im ersten Bild besteht im Kern aus einem Viergelenkgetriebe mit bestimmten Krümmungseigenschaften an der Koppelkurve. Diesen Krümmungsverhältnissen entsprechend wurde dann der Zweischlag C0-C-K hinzukonstruiert.
Sind Kurvengetriebe oder Servoantriebe mit elektronischen Kurven erlaubt, hat man sehr gute Chancen, die Bewegungsaufgabe exakt zu erfüllen, allerdings mit entsprechend komplexer Mechanismenstruktur.
Es werden dann so viele Kurvengetriebe benötigt, wie die Bewegungsvorgabe Dimensionen hat. Bei der Synthese einer Übertragungsfunktion oder einer Punktführung wird beispielsweise ein einziges Kurvengetriebe benötigt. Bei einer Punktführung mit Vorgabe der Durchlaufgeschwindigkeit oder einer Ebenenführung sind zwei Kurvengetriebe erforderlich, bei einer Ebenenführung mit Vorgabe der Durchlaufgeschwindigkeit sogar drei.
Mechanismenstrukturen findet man in unterschiedlichsten Quellen, beispielsweise:
- Lösungskatalog in OPTIMUS MOTUS
- Lehrbücher der Getriebekinematik (Volmer, Burmester, u.a.)
- VDI-Richtlinien, z.B. 2727
- DMG-Lib
- Patentrecherchen
- Eigenes Zeichnungsarchiv
- Erfahrung älterer Ingenieure
- Firmen- oder verbandsspezifische Lösungssammlungen
- Modellsammlungen von Universitäten
- Gegenstände des Alltags (Augen auf, viele Dinge wurden schon erfunden, nur für andere Zwecke)
- Brainstorming
Zeichnerische Maßsynthese
Etliche ältere Lehrbücher (z.B. Burmester, Volmer) der Getriebelehre beschreiben zahlreiche zeichnerische Verfahren, um die kinematischen Abmessungen von Mechanismen für jeweils ganz spezielle Aufgabenstellungen zu finden. Diese Verfahren werden mit Zirkel und Lineal angewendet. Heute wird man aber eher auf das CAD-System oder ein interaktives Geometrieprogramm zurückgreifen. Die gleichen Verfahren findet man in vielen unterschiedlichen Quellen wieder, auch im Internet, und sind dort unterschiedlich verständlich beschrieben.
Beispiel:
2 Endlagen des Abtriebs einer Kurbelschwinge bei vorgegebenen Gestellpunkten
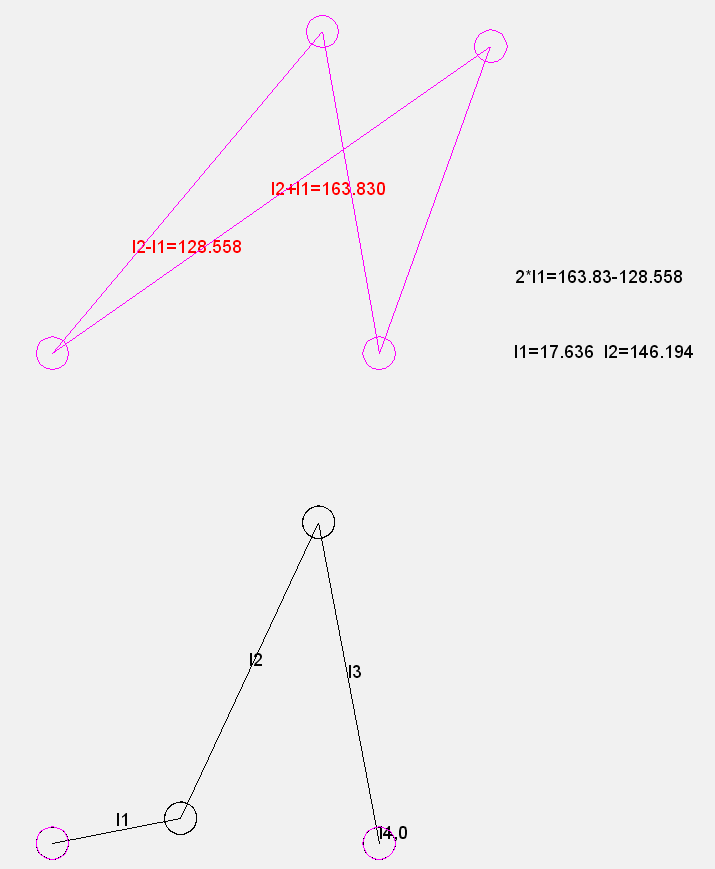
Beispiel:
Dreilagensynthese eines Viergelenkgetriebes: ein viergliedriges Koppelgetriebe mit Drehgelenken finden, bei dem die Koppel drei definierte Lagen in der Ebene durchläuft.
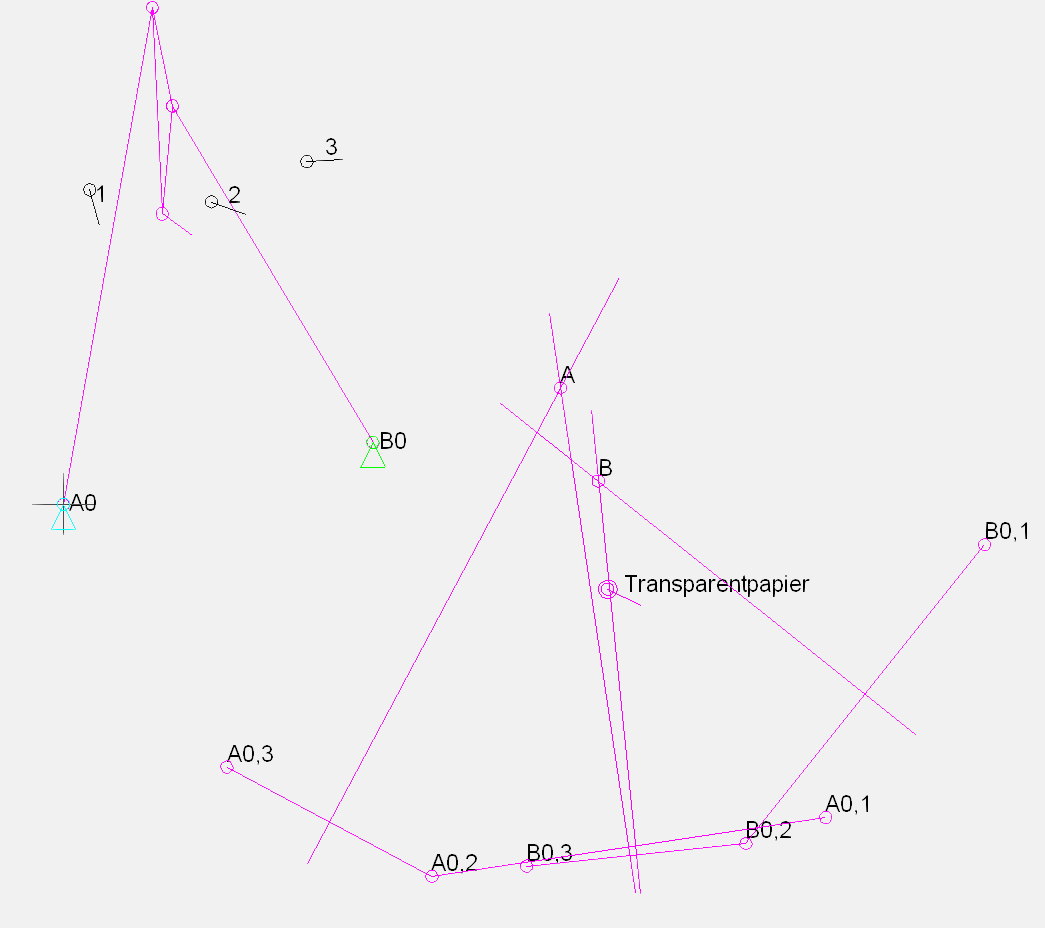
Vorgehensweise:
1. Gestellpunkte A0 und B0 auswählen
2. Ebenenlagen 1, 2 und 3 vorgeben
3. "Transparentpapier" in die Ebenenlagen 1, 2 und 3 bringen und jeweils A0 und B0 übertragen
4. Umkreise um die übertragenen A0- bzw. B0-Punkte konstruieren, Kreisradien = Lenkerlängen, Kreismittelpunkte = A bzw. B
Aus heutiger Sicht werfen die klassischen zeichnerischen Synthesemethoden jedoch einige Probleme auf:
Problem 1: Es gibt sehr viele verschiedene Verfahren für jeweils genau umrissene Voraussetzungen, und es ist extrem aufwändig, diese Verfahren alle zu lernen und zu beherrschen.
Problem 2: Die Verfahren bzw. die Erläuterungen der Verfahren sind ohne spezielle Getriebelehre-Ausbildung nur schwer verständlich.
Problem 3: Spezielle technologische Zusatzforderungen (Kräfte, Kollisionsvermeidung) können in der Regel nicht berücksichtigt werden.
Wir denken, dass es erheblich attraktiver ist, eine einzige, relativ einfache Methodik zu haben, mit der man alle Aufgaben lösen kann!
Numerische Maßsynthese
Die Idee, eine einzige Methodik für alle Arten von Mechanismensynthese zu verwenden, führt uns zur numerischen Maßsynthese.
Mit dieser Methodik optimieren wir kinematische Abmessungen einer Mechanismenstruktur, aber auch Bewegungsvorgaben, Masseverteilungen, Federparameter und Werte für beliebige andere Parameter, um die technologischen Forderungen bestmöglich zu erfüllen.
Die Summe der technologischen Forderungen wird dabei in einer oder mehreren Zielfunktionen zusammengefasst.
Die Zielfunktion ist selbst Gegenstand einer Optimierung.
Vorgehensweise (für alle Aufgabenstellungen gleich!):
1. Mechanismenstruktur auswählen
2. Variierbare Parameter festlegen
3. Zielfunktionen festlegen
4. Einfluß der Parameter auf die Zielfunktionen in verschiedenen Getriebestellungen feststellen
5. Parameter auswählen, die optimiert werden sollen
6. Anzahl Optimierungsparameter verringern (Parameterabhängigkeiten erkennen und formulieren)
7. Suchfeldberechnungen durchführen
8. Beste im Suchfeld gefundene Lösungen mit Newton- oder Suchschrittverfahren optimieren
9. eventuell Zielfunktion verbessern und Ablauf neu durchgehen
Die Zahl zu optimierender Parameter sollte so gering wie möglich gehalten werden, da die Komplexität der Syntheseaufgabe exponentiell mit der Parameterzahl steigt.
Diese einheitliche numerische Methodik ist viel leistungsfähiger und viel einfacher zu verstehen als die Vielfalt der zeichnerischen Maßsyntheseverfahren.
Gerne unterstützen wir Sie mit dieser Methodik bei der Suche nach optimalen Mechanismen!
Newton-Verfahren
Das Newton-Verfahren sucht X für die Gleichung f(X) = 0.
f ist in der Regel eine Zielfunktion, X der Vektor der Optimierungsparameterwerte.
Das Newton-Verfahren ist geeignet für numerisch stabile, relativ einfache Optimierungsaufgaben und konvergiert sehr schnell. Es erfordert die Definition N unabhängiger Zielfunktionen, wenn N Optimierungsparameter variiert werden sollen. Es ist dann anwendbar, wenn mit Sicherheit eine exakte Lösung für die Syntheseaufgabe in der Nähe der Startvorgabe existiert.
Anwendungsbeispiele:
- Ermittlung einer Koppelstangenlänge für einen maximalen Kurvenradius
- Ermittlung eines Kurbelradius und einer Koppelstangenlänge im Viergelenkgetriebe für einen gegebenen Schwingwinkelbereich psimin .. psimax am Abtriebslenker
- Lösen nichtlinearer Gleichungen im Rahmen der Verringerung der Optimierungsparameter-Anzahl (Mittel zum Auflösen der Parameterabhängigkeiten)
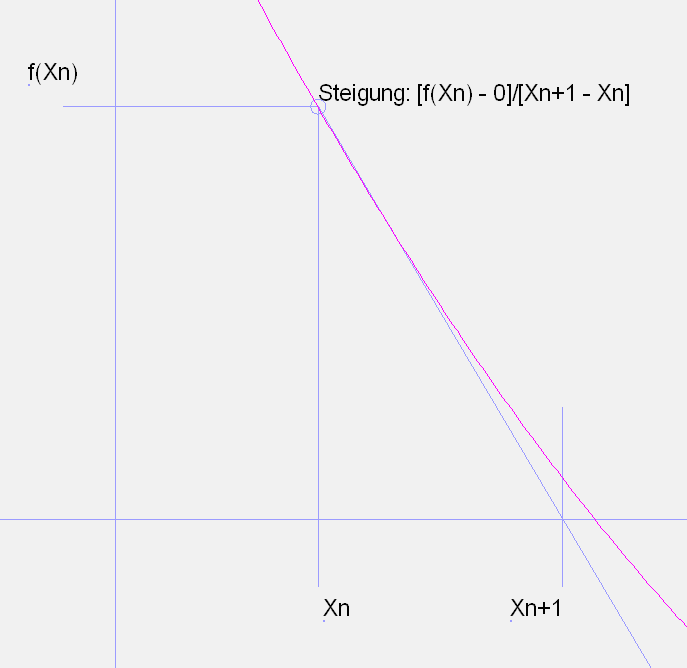
Algorithmus eindimensional:
Vorgabe: Startwert X0
Schritt: Xn+1 = Xn – f(Xn) / f'(Xn)
Algorithmus mehrdimensional:
Vorgabe: Startvektor X0
Schritt: Xn+1 = Xn – inv(A) • F(Xn)
F ist der N-dimensionale Zielfunktionsvektor.
X ist ebenfalls N-dimensional.
A ist die Jacobi-Matrix dfi / dxj
inv(A) ist die zu A inverse Matrix.
In der Regel erreicht das Newton-Verfahren mit wenigen Schritten hohe Genauigkeiten. Die Iteration kann dann durch eine feste Berechnungsfolge mit konstanter Anzahl von Iterationsschritten ersetzt werden:
Startwert X0
X1 = X0 – f(X0) / f'(X0)
X2 = X1 – f(X1) / f'(X1)
X3 = X2 – f(X2) / f'(X2)
Zur Berechnung der Ableitungen kann der Differenzenquotient
f'(X) = [f(X + h) – f(X)] / h
mit dem Variationsinkrement h verwendet werden.
Dann wird für die Newton-Iteration keine Herleitung der Ableitung f'(X) benötigt, sondern nur die zu lösende Gleichung f(X) = 0 selbst:
Startwert X0
X1 = X0 – f(X0) / [f(X0 + h) – f(X0)] • h
X2 = X1 – f(X1) / [f(X1 + h) – f(X1)] • h
X3 = X2 – f(X2) / [f(X2 + h) – f(X2)] • h
Optimierungsparameter
Für die Beschreibung der Kinematik eines Mechanismus werden oft viele Parameter benötigt. Die meisten davon sind letztlich von wenigen Formatparametern abhängig.
Für die numerische Optimierung kinematischer Abmessungen sollten ...
... möglichst wenige Parameter verwendet werden. Die Komplexität der Optimierung steigt exponentiell mit der Anzahl an Optimierungsparametern. Schon ab 4 Parametern kann die Rechenzeit so groß werden, daß eine systematische Suchfeldberechnung nicht mehr praktikabel ist.
... nur voneinander unabhängige Parameter verwendet werden. Beispiel: Soll die Summe a+b auf 0 hin optimiert werden, und sind a und b die Optimierungsparameter, ist b = -a immer die optimale Lösung, unabhängig von a.
... Parameter verwendet werden, die einen möglichst linearen Einfluss auf die Zielfunktion haben. Die Zielfunktionen sollten sich möglichst gleichmäßig mit den Optimierungsparametern ändern.
Zielfunktion
Eine Zielfunktion ist eine eindeutige Vorschrift zur Bewertung einer konkreten Mechanismenvariante, die im Syntheseablauf durchgerechnet wird.
Bei dem Newton-Verfahren entspricht die Zielfunktion einer Gleichung im Gleichungssystem, dessen Lösung gesucht wird. Bei diesem Verfahren gibt es so viele Zielfunktionen wie Optimierungsparameter.
Bei der Suchfeldberechnung oder der Suchschrittoptimierung wird nur eine skalare Zielfunktion verwendet, die von allen Optimierungsparametern abhängt. Die Zielfunktion berechnet eine einzige Zahl zur Bewertung der Mechanismenvariante. Die Optimierer suchen Mechanismen mit möglichst betragskleinen Bewertungen, d.h. sie bringen die Zielfunktion möglichst nah an 0 heran.
Die Zielfunktion sollte in Teilzielfunktionen für verschiedene Aspekte der Bewertung aufgeteilt werden, z.B. kleines Antriebsmoment, günstiger Übertragungswinkel, kleine Beschleunigung, Vermeidung von Kollisionen.
Die Teilzielfunktionen werden gewichtet und zur Gesamtzielfunktion summiert, multipliziert oder andersartig kombiniert.
Unerwünschte Eigenschaften von Mechanismen werden mit Straffunktionen belegt, z.B. Kollisionen, schlechte Übertragungswinkel. Straffunktionswerte sind 0, solange die betrachtete Mechanismeneigenschaft innerhalb vorgegebener Grenzen bleibt. Statt eines konstanten Strafzuschlags sollte eine Strafgerade aufaddiert werden, die auf der Grenze der Zulässigkeit den Wert 0 hat und mit dem Maß der Überschreitung schnell großen Werten entgegenstrebt. So wird der Optimierer vorrangig versuchen, aus dem verbotenen Parametergebiet herauszufinden.
Das Ergebnis der numerischen Optimierung, d.h. der gefundene Mechanismus ist stark von der Gestaltung der Zielfunktion abhängig.
Die Zielfunktion ist daher schrittweise zu verfeinern.
Einflussgrößenberechnung
Die Einflussgrößenberechnung (Sensivitätsanalyse) berechnet die partiellen Ableitungen aller Zielfunktionen nach allen Optimierungsparametern. Sie dient zur Ermittlung der Parameter, die am meisten Einflussauf die Zielfunktionswerte haben.
Bei der Bewertung der Ergebnisse muß die Gewichtung der Zielfunktionen berücksichtigt werden!
Beispiel:
Suche nach einem Geradführungs-Viergelenkgetriebe als Ersatz für eine Gleitführung.
Frage: Welche Abmessungen lohnen sich zu optimieren?
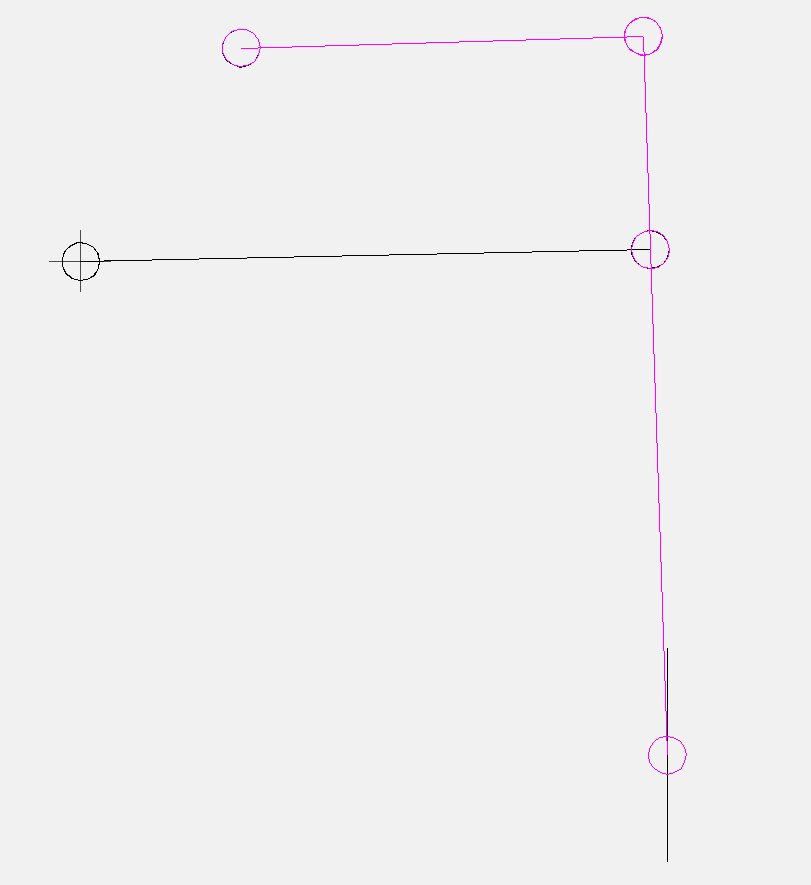
Suchfeldberechnung
Eine Suchfeldberechnung durchsucht einen definierten Wertebereich für alle Parameter und filtert die Parameterkombinationen mit den besten Zielfunktionswerten heraus. Ziel der Suchfeldberechnung ist es, gute Startvorgaben für das Suchschritt- oder das Newton-Verfahren zu finden.
Die Werte der Optimierungsparameter werden entweder systematisch mit festgelegten Schritten variiert, oder sie werden zufällig ausgewählt (Monte-Carlo-Methode). Auch wenn "Zufall" wie "unsystematisch" oder "minderwertig" klingt: die Wahrscheinlichkeit ist ziemlich hoch, mit vergleichsweise geringem Rechenaufwand in die Nähe einer guten Lösung zu kommen.
Bei einer geringen Anzahl von Optimierungsparametern und Parameterschritten empfiehlt sich die systematische Parametervariation. Die Gesamtzahl der zu berechnenden Varianten ist das Produkt aus allen Anzahlen von Einzelparameter-Varianten.
Beispiel:
Parameter a soll von 0 bis 100 mit Schrittweite 10 variiert werden (11 Einzelparametervarianten), Parameter b von 0 bis 50 mit Schrittweite 10 (6 Einzelparametervarianten). Die Gesamtanzahl an Berechnungen ist dann 6 x 11 = 66.
Bei einer sehr großen Gesamtzahl an Berechnungen entstehen so große Rechenzeiten, daß der Suchraum praktisch nicht mehr systematisch zu durchsuchen ist. Dann empfiehlt sich die Monte-Carlo-Methode.
Die gleitende Suchfeld-Berechnung arbeitet wie die Suchfeld-Berechnung, aber mit veränderlichem Mittelpunkt des Suchbereichs. Sobald eine neue Bestlösung gefunden ist, gilt diese Lösung als neuer Mittelpunkt des Suchbereichs.
Ist der Zielfunktionswert der aktuellen Lösung besser als ein vorgebbarer Grenzwert, werden die Breiten der Suchbereiche für alle Parameter mit dem gleichen, ebenfalls vorgebbaren Faktor eingeengt, damit die Optimierung in der Nähe des Optimums genauer wird!
Suchschrittoptimierung
Die Suchschrittoptimierung optimiert alle Parameter so, daß der Funktionswert einer skalaren Gesamt-Zielfunktion – ausgehend von einer Startvorgabe - optimal wird.
Sie ist für alle Optimierungsaufgaben geeignet.
Die Anzahl und Beschaffenheit der Zielfunktionen ist beliebig.
Die Suchschrittoptimierung benötigt viel Rechenzeit und findet nur lokale Optima.
Die Parameter x werden der Reihe nach um jeweils ein kleines delta vergrößert und verkleinert.
Der Parameterwert (x-delta , x oder x+delta) mit dem besten Zielfunktionswert wird für den nächsten Optimierungsschritt übernommen.
Diese Schleife wird so lange durchlaufen, bis sich die Zielfunktionswerte nicht mehr verbessern.
Anschließend werden die Parameter mit verringerten Inkrementen variiert, bis die Inkremente vorgegebene Grenzen unterschreiten.
Zusammengesetzte Optimierungen
Um numerische Optimierungen stabiler und schneller zu machen, zerlegen wir sie logisch in Teiloptimierungen, die ineinander verschachtelt werden.
Syntax:
OPTIMIERUNG = AUSDRUCK
OPTIMIERUNG = AUSDRUCK OPTIMIERUNG
AUSDRUCK = NAME
AUSDRUCK = NAME ( OPTIMIERUNG )
Beispiel:
Eine Kurbelschwinge soll eine Übertragungsfunktion von gegebener Form möglichst genau nachbilden. Auf jeden Fall soll ein Abtriebsschwingwinkel von 60 Grad eingehalten werden.
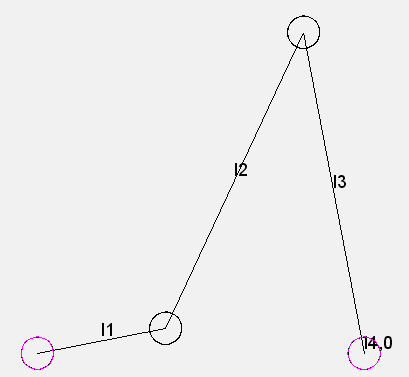
Insgesamt sollen Kurbellänge l1, Koppellänge l2 und Gestelllänge l4 variiert werden.
Die Schwingenlänge l3 wird auf einen festen Wert gesetzt. Er normiert die Größe des Mechanismus. Reines Skalieren des gesamten Mechanismus würde die Übertragungsfunktion nicht verändern.
Bei gegebener Koppel- und Gestelllänge ist der Schwingwinkel maßgeblich von der Kurbellänge abhängig.
In einer inneren Optimierungsschleife sollte also die Kurbellänge auf den Schwingwinkel 60 Grad hin optimiert werden. Dazu bietet sich das schnelle Newton-Verfahren an, weil es für diese Teilaufgabe immer eine exakte Lösung gibt, solange das Getriebe umlauffähig bleibt
In einer äußeren Schleife werden mit der Suchfeldberechnung und anschließend mit dem Suchschrittverfahren Koppel- und Gestelllänge auf eine möglichst gute Einhaltung der Form der Übetragungsfunktion hin optimiert. Für diese äußere Optimierung gibt es in der Regel keine exakte Lösung.
Die Struktur dieser Optimierung sieht so aus:
Suchfeld_l2_l4(Newton_l1),Suchschritt_l2_l4(Newton_l1)
zur Startseite von Nolte NC-Kurventechnik GmbH
Start Fachberichte Mechanismen Kinematik Kurvengetriebe Schrittgetriebe Servo/SPS Bewegungsdesign Fortbildung Service Kurvenberechnung Software Impressum Datenschutz
Struktursynthese Zeichnerisch Numerik Newtonverfahren Parameter Zielfunktion Einflussgrößen Suchfeld Suchschritt Kombioptimierung Geradführungs-Beispiel
11/06/21
• Software OPTIMUS MOTUS ® /
DasNolte ®
• Berechnung von Kurven aller Art
• Performance-Optimierung
• Trainings und Beratung
• App- und Software-Entwicklung
• SPS-Bewegungsprogramme
Kurven, Mechanismen, Bewegungsdesign. Für schnellere Maschinen. Seit 1965.
