Globoidkurven

Globoidkurven sind eine verbreitete, trotzdem aber sehr spezielle Bauform von Kurvengetrieben. In der Praxis kommen sie fast ausschließlich in Globoidkurven-Schrittgetrieben zum Einsatz, dafür werden sie aber gern und regelmäßig verwendet. Das Abtriebsglied kann auch oszillieren, also "pendeln".

Globoidkurven sind räumliche Kurven. Antrieb und Abtrieb im Globoidkurvengetriebe sind drehend, und die Drehachsen von Kurve und Abtriebsglied (Hebel oder Rollenstern) stehen senkrecht aufeinander.

Das Besondere bei Globoidkurven ist, dass die Rollenachse in der Bewegungsebene des Abtriebsgliedes liegt. Bei einem Globoidkurvenschrittgetriebe sind die Rollen sternförmig um die Drehachse des Abtriebsgliedes verteilt. Bei Kurvenscheiben und Zylinderkurven hingegen steht die Rollenachse senkrecht auf der Bewegungsebene des Abtriebs.

Während die Kurvenbahnen bei einer Zylinderkurve in einen Zylindermantel als Bezugsfläche eingebracht werden, dienen bei Globoidkurven "Tori" als Bezugsflächen. "Tori" ist die Mehrzahl von "Torus". Ein Torus ist die ringförmige Austragung eines kreisförmigen Querschnitts, wie bei einem Rettungsring, einem Schubkarren-Reifen oder einem Donut.

Meistens wird nur die innen liegende, der Kurvendrehachse zugewandte Seite der Bezugsfläche verwendet. Möglich ist aber auch, die außen liegende Seite zu nutzen, so dass der Rollenstern bzw. der Hebel innerhalb der Kurvenflanken liegt. Wegen der sternförmigen Anordnung der Rollen sehen Kurvenstege bei Globoidkurven trapezförmig aus, sind also in der Regel auf kleineren Durchmessern dicker.

Vorteile von Globoidkurven:

• Kurvenstege unten dicker als oben, hohe Biegesteifigkeit
• kompakte und steife Bauweise
• hohe Schwungmasse (Vorteil bei konstanter Antriebsdrehzahl)

Nachteile von Globoidkurven:

• hohe Eigenträgheit (Nachteil bei Antrieb mit Servo oder Not-Stop)
• schwierig herzustellen (nur 5-achsige Bearbeitung), damit teuer
• sehr komplizierte räumliche Geometrie der Kurvenflanke, muss bei Austragungen im 3D-CAD beachtet werden
• in der Regel immer auch Gleitanteil beim Abwälzen der Rolle auf der Kurve, begünstigt Verschleiß

Die räumliche Geometrie ist bei Globoidkurven noch komplizierter zu handhaben als bei Zylinderkurven.

Wir berechnen Globoidkurven mit selbst entwickelter Software seit sehr vielen Jahren und kennen uns entsprechend sehr gut damit aus. Gerne unterstützen wir Sie bei der Auslegung Ihrer Globoidkurven und bei der Aufbereitung genauer NC-Daten und CAD-Austragungen mit unserer Software OPTIMUS MOTUS und unseren Beratungs- und Berechnungsdienstleistungen.

Direkt zu ...

• Abwicklungsdarstellung
• Koordinatensysteme
• Herstellung
• Fasen
• CAD-Aufbereitung
• Fehlermöglichkeiten
• spezielle Bauformen

zur Startseite von Nolte NC-Kurventechnik GmbH

> English version of this page

Abwicklungsdarstellung

Bei Globoidkurven sind Abwicklungsdarstellungen nicht unbedingt üblich. Problematisch dabei ist nämlich, dass die Kurvenflanken in zwei Richtungen abgewickelt werden müssen, was immer zu Verzerrungen in der Darstellung führt.

Der Torus als "Träger" der Kurvenflanken wird zunächst unter Annahme eines Bezugsdurchmessers zu einem Zylinder langgestreckt. Das staucht außen liegende Bereiche des Torus und streckt die inneren, verzerrt also die Geometrie der Kurvenflanken. Steigungen und Krümmungen erscheinen in der Abwicklung nicht mehr so wie bei der räumlichen Betrachtung des ursprünglichen Torus. Anschließend wird der Zylinder entweder in die Ebene gestreckt oder projeziert.

Leider hat eine Kurvenflanke eine Höhe, so dass Tori in einem ganzen Durchmesser-Bereich abgewickelt werden müssen ...

Ein ähnliches Problem hat man übrigens, wenn man eine Weltkarte verzerrungsfrei in der Ebene darstellen will. Verzerrungsfrei geht das nämlich gar nicht.

Um die Abwicklung zu veranschaulichen, hier einige Bilder:

Zunächst der vollständige Torus, der als Bezugsfläche für die Kurvenflanken dient:

Von diesem Torus braucht man bei fast allen Globoidkurven-Berechnungen aber nur die innen liegenden Bereiche:

Diese "Felge" streckt man in die Länge. Dabei verwendet man den Bezugsdurchmesser D (siehe Bild weiter unten). Es entsteht eine Rinne der Länge D•pi:

Der Bezugsdurchmesser D ist ein mittlerer Wert, um näherungsweise den Kurven-Durchmesserbereich abzudecken, den die Kurvenflanke ausnutzt.

Die zylindrische Rinne streckt man dann entweder in die Ebene aus (Alternative 1, im Bild links), oder man projeziert sie in die Ebene (Alternative 2, im Bild rechts):

Die Projektion hat den Vorteil, dass die Ausdehnung der Kurvenbahnen in der Breite (längs zur Kurvenachse) erhalten bleibt, aber den Nachteil, dass die Kurvenbahnen für die Darstellung noch einmal verzerrt werden.

Trotz der auftretenden Verzerrungen finden wir die Abwicklungsdarstellung praktisch und verwenden sie für die Bewertung von Kurven. Meist sind die Verzerrungen so klein, dass man noch gut erkennen kann, ob Kurvenstege zu dünn, Steigungen zu groß und Krümmungsradien zu klein werden.

Wenn man die Verhältnisse jedoch genau betrachten will, hilft nur der Blick auf die räumliche Geometrie der Kurvenflanken:

Wie bei den Zylinderkurven ändern sich Steigungen, Krümmungen und Stegdicke längs der Kontaktlinie zwischen Rolle und Kurve, also mit der Höhe der Kurvenflanke.

In der Software OPTIMUS MOTUS werden die Kurvenflanken auf mehreren Bezugs-Tori genau berechnet. Man erhält ein exaktes 3D-Modell des Rollenspurvolumens, das auch für hochpräzise Bearbeitungsverfahren geeignet ist.

Insbesondere rechnen wir auch bei Globoidkurven die Werkzeugradius-Korrektur in die NC-Daten ein, so dass sich die Werkzeugkosten erheblich reduzieren lassen.

zurück zum Start der Seite

Koordinatensysteme

Für die Betrachtung von Globoidkurven benötigt man geeignete Koordinatensysteme. Sie können bei Berechnung, im CAD, bei der NC-Aufbereitung und der Werkzeugmaschine unterschiedlich sein. In der Praxis entstehen leicht Mißverständnisse und Fehler. Das betrifft vor allem die Vorzeichen der Achsrichtungen bei Werkzeugmaschinen.

Bei der Kurvenberechnung erzeugen wir zunächst Metadaten in einem neutralen Format. Mit standardisierten oder kundenspezifisch entwickelten Postprozessoren werden diese Daten dann konkret für die Fertigung aufbereitet.

Für die NC-Metadaten verwenden wir folgendes Koordinatensystem:

X = Kurvendrehachse, hauptsächliche Hubrichtung
Y = Mittenauswanderungsachse, senkrecht zu X und zu Z
Z = Höhenachse, senkrecht zu X, in der Bewegungsebene des Abtriebsgliedes
A = Kurvendrehwinkel bzw. Rundtischwinkel nach der Linke-Hand-Regel (wegen der kinematischen Umkehr bei der Berechnung)
B = Schwenkwinkel der Rollenachse

Folgende Animation zeigt diese Achsen. Nacheinander bewegen alle Achsen das Werkzeug.

Verfolgen Sie die Koordinaten X, Y, Z, A und B am unteren Bildrand!

Um die Transformation auf eine spezielle Werkzeugmaschine zu ermitteln, lassen Sie die Maschine am besten live in die unterschiedlichen Koordinatenrichtungen fahren und notieren Sie, welche Achse an der Maschine in welche Richtung läuft, wenn sich das Werkzeug relativ zum Werkstück bewegt wie in der Animation.

Bei den Werkzeugmaschinen sind jedoch zwei grundsätzlich unterschiedliche Anordnungen zu unterscheiden. Die Achsbezeichnungen A und B beziehen sich dabei auf das von uns verwendete Standard-Koordinatensystem.

1.) Das Werkzeug schwenkt mit der B-Achse relativ zum Gestell, und die Kurve dreht mit der A-Achse relativ zum Gestell. So ist es in der Animation dargestellt.

2.) Das Werkzeug schwenkt nicht relativ zum Gestell. Statt dessen schwenkt der Teilapparat, der die Kurve mit der A-Achse dreht, selbst mit der B-Achse relativ zum Gestell.

Im zweiten Fall sind bei der Transformation der Koordinaten für die NC-Steuerung nicht nur Achsbezeichnungen und die Vorzeichen anzupassen, sondern auch die Koordinatenwerte selbst umzurechnen. Es gehört zu unserem Leistungsspektrum, kundenspezifische Postprozessoren für solche NC-Koordinaten-Transformationen inklusive geometrischer Umrechnungen zu entwickeln.

Beim Export von CAD-Daten werden Rundtischachse A und Schwenkachse B nicht benötigt. Die Globoid-Kurvenbahnen werden vielmehr durch 3D-Splines mit X/Y/Z-Koordinaten dargestellt, die sich auf ein Kurvenkoordinatensystem beziehen.

Die X-Achse des Kurvenkoordinatensystems entspricht der Drehachse der Kurve.
Y (senkrecht zu X) ist bei phi=0 (Anfang Bewegungsplan) mit der Y-Achse der NC-Metadaten identisch.
Z wird nach der Rechte-Hand-Regel ermittelt: Z = X x Y.

Das Kurvenkoordinatensystem bei Globoidkurven ist das gleiche wie bei Zylinderkurven.

Die Nullpunkte bei NC-Metadaten und CAD-Daten liegen auf der Kurvendrehachse.

zurück zum Start der Seite

Herstellung

Globoidkurven werden auf Werkzeugmaschinen mit 5 synchron gesteuerten Achsen hergestellt. Der Rundtisch (bzw. ein Teilapparat) werden benötigt, um die Drehung der Kurve um ihre Achse abzubilden. Zusätzlich muss die Schwenkbewegung des Werkzeugs relativ zur Kurve abgebildet werden.

Eine einfache, aber kostenintensive Strategie ist, Globoidkurven mit Werkzeugen herzustellen, die den Durchmesser der Rolle haben. Bei großen Rollen ist das aber teuer. Auch bei kleineren Rollen ist immer ein Werkzeug mit Rollen-Nenndurchmesser erforderlich. Nachgeschliffene Werkzeuge wären zum Schlichten nicht mehr zu verwenden. Bei Nutkurven würde man zudem beide Flanken mit unterschiedlicher Qualität herstellen (Gegenlauf/Gleichlauf), und beim Fräsbeginn einer Kurve mit oszillierendem Abtrieb würde ein Absatz entstehen, der den Bewegungsablauf empfindlich stört. Für Globoidkurven bieten CNC-Steuerungen nach unserem Kenntnisstand keine Werkzeugradius-Korrektur an.

Wir generieren NC-Daten für Globoidkurven deshalb entweder direkt für einen definierten Werkzeugdurchmesser (inklusive Werkzeugradius-Verrechnung), oder wir erzeugen parametrische NC-Programme mit eingebauter Werkzeugradius-Korrektur. Mit dieser parametrischen Programmierung wird der konkrete Werkzeugdurchmesser an der CNC-Maschine eingegeben.

Mit der Werkzeugradius-Verrechnung von OPTIMUS MOTUS können also die Werkzeugbeschaffungskosten erheblich gesenkt werden!

Beim Schneiden einer Globoidkurvenflanke mit einem Werkzeug ungleich dem Rollendurchmesser in einem Schnitt entstehen Abweichungen am Profil. Es bleibt zuviel Material stehen. Diese Abweichungen sind umso größer, je steiler die Kurvenbahn ist, je weiter der Profilpunkt vom Wirkradius am Hebel bzw. Rollenstern entfernt ist, und je größer die Differenz zwischen Werkzeug- und Rollendurchmesser ist. Der Effekt ist ähnlich wie bei den Zylinderkurven.

Es ist aufwendig, Kurvenflanken "abzuzeilen", die Kurvenflanke also mit einem balligen Werkzeug auf vielen Höhen der Kurvenflanke zu fräsen, und es entstehen Längsrillen, die das Tragbild zwischen Rolle und Kurve beeinträchtigen. Das Abzeilen ist theoretisch genauer, wegen des Aufwands und des Oberflächen-Qualitätsnachteils trotzdem aber unattraktiv.

Wir schätzen diese Profilabweichungen mit der Software OPTIMUS MOTUS auch bei Globoidkurven ab. So ermitteln wir, bis zu welchem Werkzeugdurchmesser die Abweichungen unkritisch sind. Oft sind die Profilabweichungen klein, auch bei größerer Differenz Rollendurchmesser-Werkzeugdurchmesser.

Bei balligen Kurvenrollen ist der Durchmesser an den Rändern etwas kleiner ist als in der Mitte, und sehr oft verjüngt sich die Rolle entlang ihrer Achse schneller, als der Profilfehler an der Kurve zunimmt. Im Querschnitt sieht der Kontakt Rolle-Kurve etwa so aus:

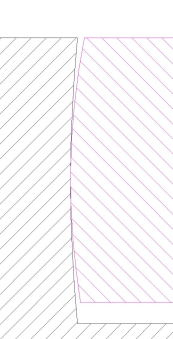
Wenn die Profilabweichung längs der Rolle zu stark steigt, läuft die Rolle nur auf der Kante bzw. klemmt in einer Kurvennut fest.

Die Software OPTIMUS MOTUS kann NC-Daten fünfachsig numerisch nachoptimieren, um Profilabweichungen zu minimieren.

zurück zum Start der Seite

Fasen

Beim Fräsen von Globoidkurvenflanken bleiben scharfe Kanten am Rand der Kurvenflanke stehen, die oft mit der Flex oder der Feile entgratet werden. Der Aufwand dafür ist hoch, und die von Hand bearbeiteten Kanten sehen nicht schön aus.

Mit speziellen Postprozessoren in unserer Software OPTIMUS MOTUS geben wir NC-Daten für kegelförmige Werkzeuge aus, um die Globoidkurvenflanken NC-gesteuert zu entgraten.

Man erhält gleichmäßige, saubere Fasen mit konstanter Breite. Solche Kurven sehen hochwertig aus, und man kann die Kosten für das Entgraten gering halten.

CAD-Aufbereitung

Für ein korrektes CAD-Modell einer Globoidkurve berechnen wir alle Kurvenflanken auf mehreren Bezugs-Tori, also auf verschiedenen Höhen der Kurvenflanke, exakt und tragen mit diesen Raumkurven ein "Rollenspurvolumen" aus. Das ist die Spur, die die Rolle beim Durchlauf durch den Kurvenkörper durchläuft.

Um ein Volumenmodell der Kurve zu erhalten, zieht man das Rollenspurvolumen vom Kurvenrohling ab.

Heute werden NC-Daten immer häufiger von Volumenmodellen abgeleitet, die meist im Step-Format ausgetauscht werden. Deshalb sind korrekte Volumenmodelle von Kurven heute sehr wichtig für die Fertigung.

Der Teufel steckt bei den Austragungen im Detail. Vereinfachte Austragungen, die z.B. nur auf der Mittelpunktsbahn der Rolle beruhen, sehen zwar richtig aus, weichen aber von der korrekten Form der Kurvenflanke ab.

Unsere Software OPTIMUS MOTUS liefert exakte Daten, die für fertigungstaugliche Austragungen geeignet sind.

zurück zum Start der Seite

Fehlermöglichkeiten

Die Berechnung und Herstellung von Globoidkurven ist definitiv etwas für Kurven-Spezialisten.
Wenn die Berechnung oder die Fertigung die Besonderheiten der räumlichen Geometrie der Kurvenflanken nicht beherrscht, kommen schnell unbrauchbare Kurven dabei heraus. Dann ist Erfahrung und analytisches Denken gefragt, um den Fehlern auf die Spur zu kommen.

Bei offenen Globoidkurven läuft die Rolle immer irgendwie über die Kurvenflanke, aber das Tragbild zwischen Kurve und Rolle stimmt nicht, wenn Berechnungs- oder Fertigungsfehler aufgetreten sind. Es droht dann großer Verschleiß, und die Übertragungsfunktion des Kurvengetriebes wird verfälscht. Das Kurvengetriebe tut dann nicht mehr, was es soll. Offene Globoidkurven kommen in der Praxis relativ selten vor.

Formschlüssige Globoidkurvengetriebe (Nutkurven oder Stegkurven, meistens Schaltkurven) klemmt das Kurvengetriebe in der Regel im Fehlerfall.

Bei Globoidkurven heißt es: korrekt rechnen, fertigen und montieren!

Falls man bei Globoidkurven doch einmal Probleme hat, hilft vielleicht folgende Liste potenzieller Fehler:

• mit falschen kinematischen Abmessungen gerechnet
• Exzenterbolzen eingesetzt, aber bei Berechnung nicht berücksichtigt
• Werkzeugdurchmesser zu klein für Steigung, Flankenhöhe und Rollendurchmesser
• falsche Grundkinematik der Werkzeugmaschine angenommen
• Koordinaten nicht korrekt transformiert, insbesondere die Mittenauswanderungsachse
• keine korrekte Äquidistante gerechnet, sondern NC-Daten nur achsparallel verschoben
• räumliche Geometrie des Kontakts Rolle/Kurve nicht korrekt berücksichtigt
• falscher Austragungstyp im CAD verwendet
• Raumkurven für die Austragung im CAD nicht korrekt ermittelt
• Rundtischachse hat Umkehrspiel

zurück zum Start der Seite

Spezielle Bauformen

Mit unserer Software OPTIMUS MOTUS berechnen wir auch spezielle Varianten von Globoidkurvengetrieben.

Beispielsweise kann man die Rollen auf dem Rollenstern eines Schrittgetriebes kröpfen, so dass der Winkel zwischen der Rollendrehachse und der Rollenstern-Drehachse nicht 90 Grad beträgt, sondern zwischen 0 Grad und 90 Grad liegt.

Oder man optimiert den Kontakt zwischen Rolle und Kurve dadurch, dass die Kurvenbahn selbst ballig ausgeführt wird:

Der Rollenmantel darf dann auch weniger konkav ausgeführt sein, oder sogar zylindrisch.

Die Ebene, in der der Rollenstern bzw. die Hebel drehen, kann relativ zur Kurvendrehachse gekippt werden:

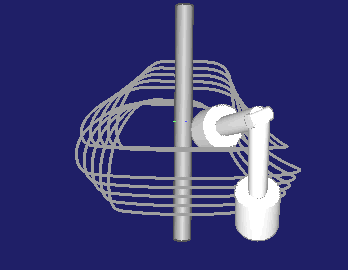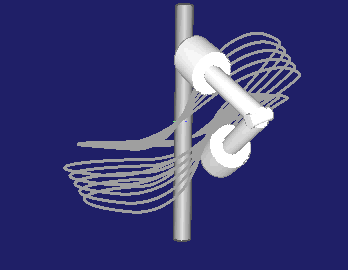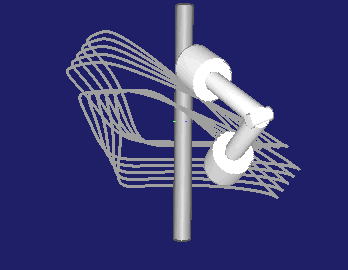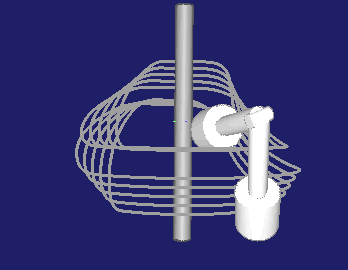
Bei allgemeinen 3D-Kurvenberechnungen mit unserer Software OPTIMUS MOTUS können

• die räumliche Bewegung der Kurve
• die räumliche Bewegung der Rollen
• die Balligkeit der Rolle
• und die Konizität der Rolle

frei festgelegt werden, so dass der Ingenieur bei der Gestaltung von Kurvengetrieben sehr kreativ sein darf.

OPTIMUS MOTUS wird auch in Spezialfällen Daten für die CAD-Modellierung und die NC-Bearbeitung liefern.

zurück zum Start der Seite

zur Startseite von Nolte NC-Kurventechnik GmbH

Start Fachberichte Mechanismen Kinematik Kurvengetriebe Schrittgetriebe Fortbildung Servo/SPS Bewegungsdesign Software Service Kurvenberechnung Impressum Datenschutz
Abwicklung Koordinaten Herstellung Fasen CAD-Daten Fehlermöglichkeiten Spezielles

> zu unseren Kontaktdaten