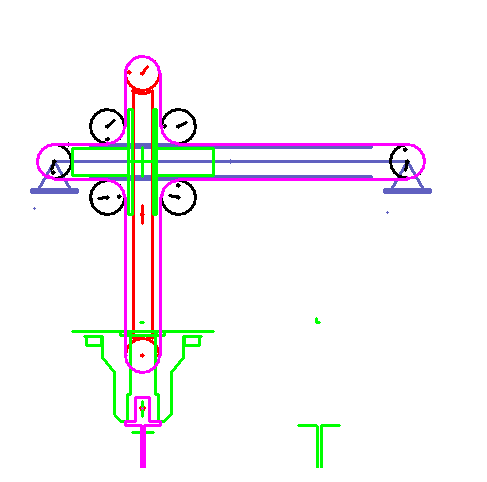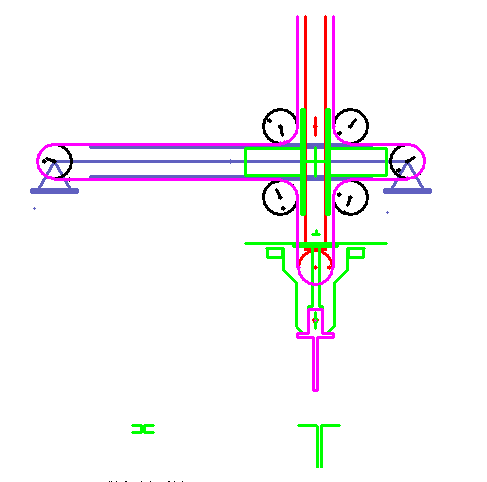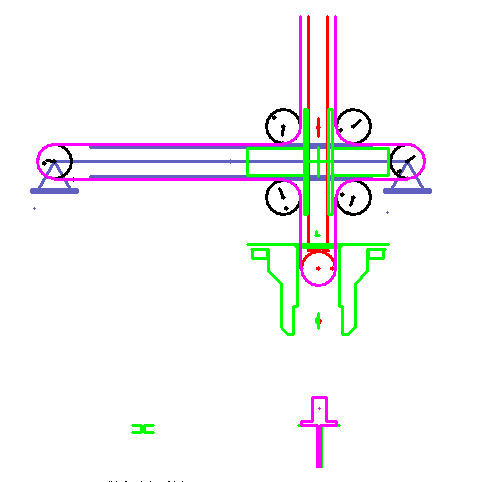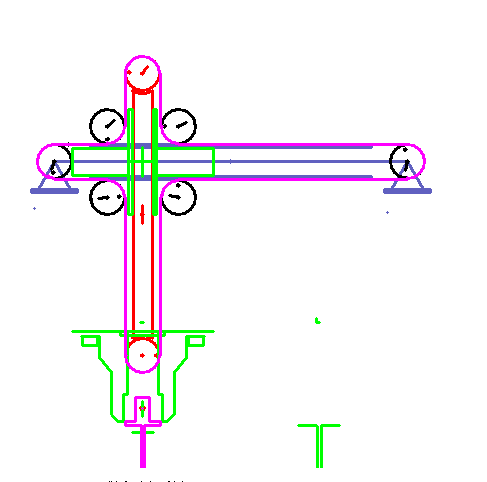
Bewegungsdesign

Bewegungsdesign ist die Planung und Feingestaltung von Bewegungen in Maschinen. Dies ist seit über 45 Jahren unser Kernthema.

Bewegungsdesign macht Maschinen schneller, leiser, Energie sparender und verfügbarer, bei gleichen Herstellkosten.

Bewegungsdesign geht dabei sehr weit über die einfache Anwendung festgelegter Bewegungsgesetze (z.B. Polynom 5. Grades oder Modifizierte Sinuslinie) hinaus. Mit “Bewegungsdesign” ist vielmehr ein umfassender Optimierungsprozess gemeint, in dem die Bewegungen im Detail so gestaltet werden, dass gesteckte Optimierungsziele bestmöglich erreicht werden. Insbesondere wird auch die charakteristische Form eines Bewegungsgesetzes umgestaltet, wenn es von Vorteil ist. Und wir optimieren Bewegungen auch mit numerischen Methoden, wenn es drauf ankommt.

Typisch ist die Optimierung auf hohe erreichbare Taktzahlen hin, häufig sind aber auch die Baugrößen von Servomotoren, Getrieben und Umrichtern, die Lebensdauern von Kurven und Rollen oder die dynamischen Gestellkräfte im Fokus der Optimierung. Auch Kombinationen von Kriterien sind möglich.

Je besser das Bewegungsdesign, desto leistungsfähiger die Maschinen. Und in der Konkurrenzsituation kommt es eben gerade auf die letzten Prozentpunkte an, um den Auftrag für sich zu gewinnen. Das gilt gleichermaßen für klassisch kurvengesteuerte Anlagen wie auch für flexible Konzepte mit Servosteuerungen.

Bewegungsdesign trägt eine neue Qualität in Ihre Maschinen hinein und bringt sie auf das nächste oder übernächste Level.

Bewegungsdesign ist ein Muss für Hersteller von Maschinen, bei denen Taktzahl, Laufruhe, Reproduzierbarkeit und Verfügbarkeit eine Rolle spielen.

Unsere Software OPTIMUS MOTUS bietet in einem grafischen Editor extrem vielfältige und leistungsfähige Methoden an, um Bewegungen dynamisch zu optimieren.

Profitieren Sie von unserer über 45-jährigen Erfahrung und unserem ständigen Drängen nach vorn auf diesem Gebiet!

Wir unterstützen Sie mit Beratung, Bewegungsauslegung und Software.

Außerdem geben wir unser Know How im Bewegungsdesign in Form von Seminaren weiter. Dabei greifen wir auch Ihre konkreten Projekte auf.

Direkt zu ...

• Beispiele
• Allgemeines
• Bewegungsgesetze
• Bereichserweiterung
• Kollisionsoptimierung
• Energetische Optimierung
• HS-Profile
• Kubische Splines
• Warum Bewegungsdesign wichtig ist
• Software
• Berechnung

zur Startseite von Nolte NC-Kurventechnik GmbH

> English version of this page

Praxisbeispiel: Delta-Roboter für Pick&Place oder Führungsbewegung

• Vorgabe der Bahnkurve mit Überschneidungen in X / Y
• Berücksichtigung der Nichtlinearität des Mechanismus
• Optimierung der Beschleunigungen und der Belastung beider Motor-Getriebe-Kombinationen

Ziele:

• Bestmögliche Ausnutzung der Antriebe
• Taktzahl maximieren
• Schwingungen am Greifer vermeiden durch weiche Bewegungen

Praxisbeispiel: Sammelscheibe mit Eintaktrechen in einer Verpackungsmaschine

Ein Servomotor mit Getriebe treibt eine mechanische Schaltkurve an, die eine Sammelscheibe schaltet. Ein Rechen (in der Animation als grüner Finger dargestellt) schiebt Einzelartikel in die Sammelscheibe ein. Zwischen zwei Einzelartikeln dreht die Sammelscheibe eine Teilung weiter.

Für die Schaltbewegung sind nur 45 Millisekunden Zeit vorgesehen!

Durch die Kombination von Servo und mechanischer Kurve werden die Antriebsbelastungen aus Eigenträgheiten (Motor+Getriebe) und Lastträgheit (Sammelscheibe) entzerrt, so dass die Taktzahl gesteigert werden kann.

Beschleunigungen, Kräfte und Momente werden durch Simulation und Kollisionsbetrachtung verringert.

Praxisbeispiel: Einrichtung zum Stapeln von Büchern

• 10 synchrone Servoachsen
• Große Vielfalt an Formaten und Stapel-Optionen
• Optimale Bewegungsgestaltung mit ruckfreien Bewegungsgesetzen für alle Formatvarianten mit Berücksichtigung von Kollisionen

Ziel:

Taktzahl maximieren für alle Formatvarianten, optimale Ausnutzung der Mechanik für alle Formate

Anmerkung: Diese Animation haben wir schon 1998 erstellt. Mit der dynamischen Optimierung komplexer Bewegungssteuerungen mit Servoantrieben in Abhängigkeit von Formatparametern befassen wir uns seit über 20 Jahren!

Praxisbeispiel: Pick&Place mit 2 gestellfesten Servoantrieben und Riementrieb

Eine Gantry-Kinematik mit zwei gestellfesten Antrieben und Riemen bewegt einen Greifer, der Bauteile zu greift und montiert.

• Schwingungen durch die Elastizität des Riemens und der lamellenartigen Artikel selbst würden das Einsetzen der Artikel behindern.
• Speziell gestaltete, weiche Bewegungen verringern die Schwingungsanregung und erlauben höhere Taktzahlen.

Beispiel zu dieser Mechanik: Verringerung der Beschleunigung von 126 m/s² auf 17 m/s².

Praxisbeispiel: Bändertransport für Schokoriegel

Schokoriegel werden mit Servobändern aus einer Gießmaschine an die nachfolgende Verpackungsmaschine gegeben.

Gleichzeitig werden die Schokoriegel durch Versatzbewegungen auf konstanten Abstand gebracht.

Bei den geforderten Taktzahlen müssen die Beschleunigungen der Servobänder minimiert werden, damit die Artikel wegen der geringen Reibung der Transportbänder nicht verrutschen.

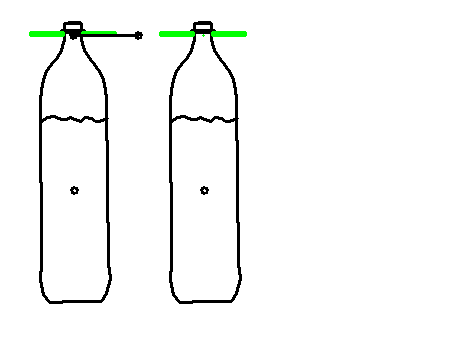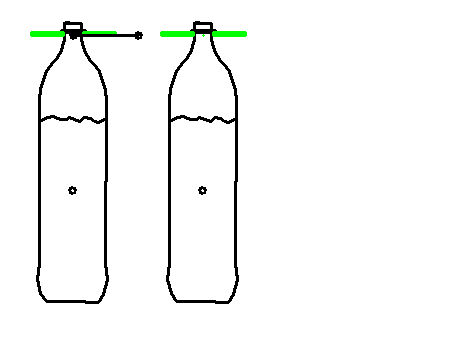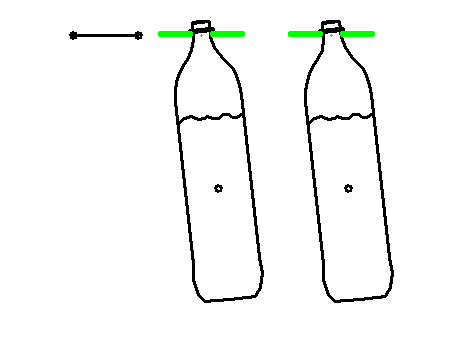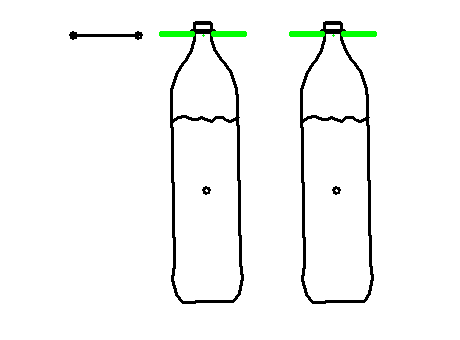
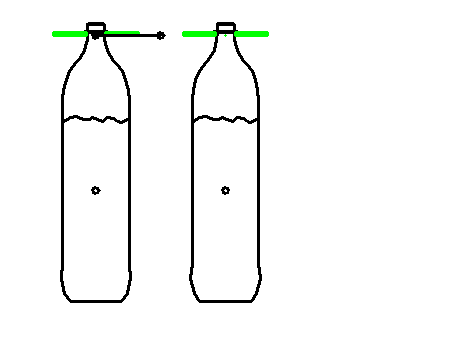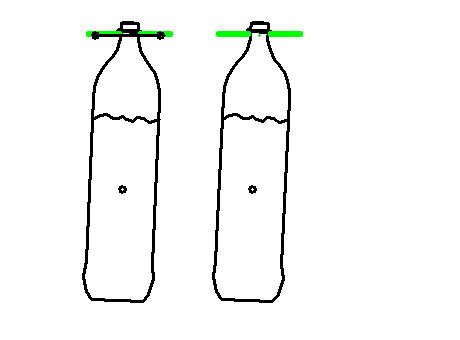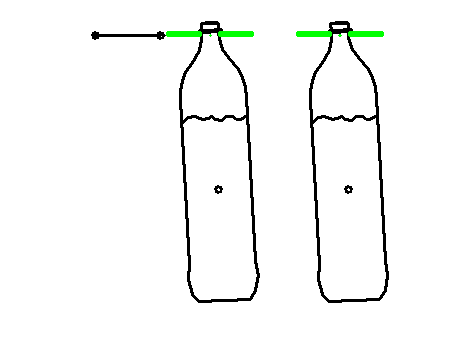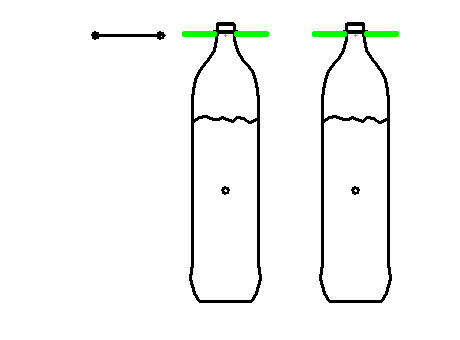
Praxisbeispiel: Anti-Schwappbewegung beim Transport von Flüssigkeiten

Artikeltransport mit Servo und Kette in einer Abfüllmaschine (Becher oder Flaschen).

Ansatz 1 mit konventioneller Bewegungsgestaltung (z.B. Modifizierter Sinus oder Polynom 5. Grades):

Die Behälter selbst schwingen,  oder die Flüssigkeit in den Behältern schwappt mit sehr niedriger Eigenfrequenz.

Problem:

Mit “normalen” Bewegungen (ruckfrei, Polynom 5. Grades oder ähnliches) können die Eigenschwingungen nicht ausreichend reduziert werden.

Ansatz 2: spezielle Bewegungsgestaltung für niedrige Eigenfrequenz:

Durch zwei spezielle Verfahren der Bewegungsgestaltung für sehr niedrige Eigenfrequenzen können wir die resultierenden Schwingungen weitgehend bzw. vollständig eliminieren.

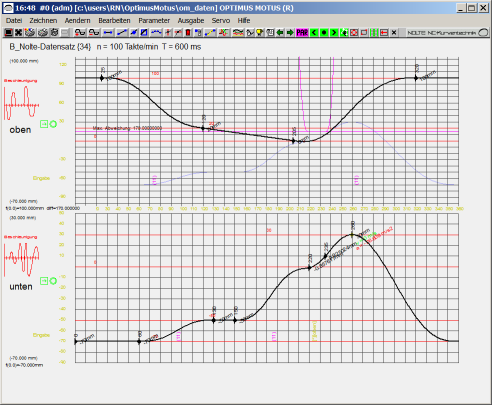
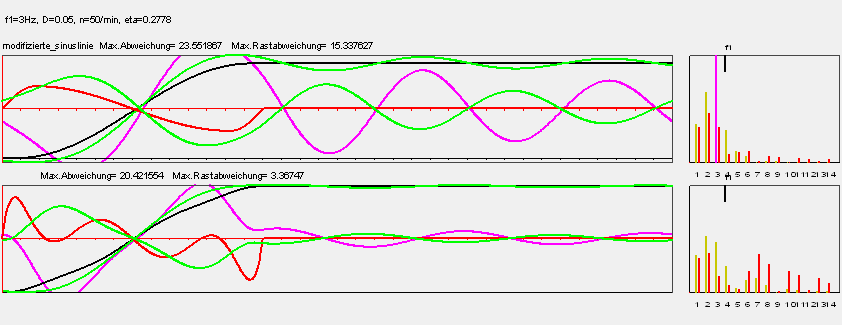
Das obere Diagramm zeigt in schwarz die durch das Schrittgetriebe oder den Servo vorgegebene Bewegung mit der bekannten und oft verwendeten Modifizierten Sinuslinie, die immerhin ruckfrei ist. Magentafarben ist dargestellt, wie die Flasche bzw. die Flüssigkeit darauf reagiert. Mit dem Polynom 5. Grades sähe das übrigens fast genauso aus.

Das untere Diagramm zeigt die nach dem ersten speziellen Verfahren optimierte Bewegung. In schwarz ist wieder die Schaltbewegung von Servo bzw. Schrittgetriebe dargestellt, magentafarben die Reaktion des Schwappguts. Die Amplitude der nachwirkenden Schwingung in der Rast ist schon um fast 80% zurückgegangen.

Mit einem von uns entwickelten weiteren Verfahren, das auch Dämpfungen berücksichtigt, können wir auch diese Restschwingungen noch eliminieren.

Damit sieht die Bewegung so aus:

Durch den speziellen Ansatz kann das Nachschwingen der Flaschen bzw. der Flüssigkeit mit der Eigenfrequenz unterbunden werden.

Fazit: Bewegungsdesign …

• macht Maschinen schneller
• vermeidet Ausfallzeiten durch Verringerung störender Schwingungen
• verlängert die Lebensdauer
• ermöglicht kleinere und günstigere Antriebe
• spart Energie

Wir unterstützen Sie gerne beim Bewegungsdesign, um Ihre Maschinen schneller, leistungsfähiger, schwingungsärmer und sparsamer zu machen!

zum Start der Seite

Allgemeines

Die optimale Bewegungsgestaltung hängt sehr stark von der jeweiligen Aufgabenstellung ab. Generell werden Kurven und Servoantriebe dynamisch auf möglichst große Leistung hin optimiert.

Leistung bedeutet

• hohe Taktzahl
• geringer Verschleiß
• präzise Verarbeitung des Produkts
• ruhiger Lauf

In der Regel bedingt die Optimierung eines dieser vier Kriterien die Verbesserung der anderen drei.

Bewegungsoptimierung bedeutet, für folgende und eventuell weitere Kriterien den bestmöglichen Kompromiß zu finden:

• Beschleunigungsmaxima am Abtrieb
• Beschleunigungsverlauf am Abtrieb
• Ruckfunktion am Abtrieb
• Schwingungsanregung
• Maximales Antriebsmoment
• Verlauf des dynamischen Antriebsmoments (Antriebsrückwirkung)
• Effektives Antriebsmoment
• Gestellkräfte
• Kurvenlebensdauer
• Rollenlebensdauer
• geringer Energieumsatz

Es gibt kein absolut bestes Bewegungsgesetz und keine absolut beste Bewegungsauslegung. Die Güte einer Bewegungsauslegung kann nur in Bezug auf einen bestimmten Mechanismus mit bestimmten dynamischen Eigenschaften bewertet werden. Für den festliegenden Mechanismus muß also festgelegt werden, wie die einzelnen Bewertungskriterien im Rahmen der Bewegungsoptimierung gewichtet werden sollten. Für diese Gewichtung ist oft eine gewisse Erfahrung mit den dynamischen Eigenschaften der eigenen Maschinen und mit Bewegungsoptimierung im allgemeinen hilfreich.

Wir optimieren Bewegungen mit folgenden Maßnahmen:

• Bewegungsgesetzauswahl und -gestaltung
• Wendepunktverschiebung
• Randwertanpassung
• Gestaltung allgemeiner Sinuskombinationen
• Gestaltung allgemeiner Polynome
• Gestaltung allgemeiner Polynomsplines
• Gestaltung und numerische Optimierung von HS-Profilen
• Bereichserweiterung
• dynamisch ausgewogene Verteilung der Übergangszeiten
• Kollisionsoptimierung
• numerische Optimierung der Bewegungsdiagramm-Parameter

Durch die geeignete Bewegungsgesetzauswahl schaffen Sie die Grundlage für die Optimierung, weil die einzelnen Bewegungsgesetze von sich aus unterschiedliche Gewichtungen in den Einzelbewertungskriterien setzen. Dabei kann auch die charakteristische Form des Bewegungsgesetzes verändert oder völlig neu gestaltet werden, wenn es von Vorteil ist.

Die Wendepunktsverschiebung betont Start bzw. Ende einer Bewegung und verlagert das Innere des Übergangs zeitlich vor oder zurück.

Das Bild zeigt links ein symmetrisches Bewegungsgesetz mit lambda = 0.5, rechts ein unsymmetrisches mit Wendepunktsparameter lambda = 0.3:

Mit Randwertanpassungen werden Geschwindigkeit, Beschleunigung und ggf. weitere Ableitungen in den Übergangspunkten zwischen den Abschnitten stetig gehalten.

Allgemeine Sinuskombinationen, allgemeine Polynome, allgemeine Polynomsplines und HS-Profile sind jeweils sehr leistungsfähige Ansätze zur Anpassung der Bewegungen an die dynamischen Eigenschaften der Mechanismen. Mit diesen Methoden holt man die entscheidenden Prozente an Performance heraus!

Die Bereichserweiterung (auch “Hubzeit-Verlängerung” genannt) verlängert Bewegungsabschnitte zeitlich über den theoretisch vorgesehenen Zeitrahmen hinaus, so dass konkurrierende Bewegungen sich im Rahmen vorgegebener Toleranzen überlappen. Wichtig ist, die voneinander abhängigen Bewegungsabschnitte zeitlich so zu verteilen, dass alle Einzelmechanismen ("Achsen") im Vergleich und jeder Einzelmechanismus über den Zyklus hinweg dynamisch gleichwertig belastet ist. Die Belastungen sollten insgesamt ausgewogen verteilt sein. Das klingt banal, aber man benötigt eine leistungsfähige Mechanismensoftware, um die Verteilung der Lasten über der Zeit und über die Achsen prüfen zu können. Die Verteilung zu schätzen, ist praktisch unmöglich. Bewegungspläne, die nur nach der Erfahrung der Konstrukteure aufgestellt wurden, sind in der Praxis oft weit entfernt von der Ausgewogenheit. In solchen Fällen gibt es immer viel Potenzial, die Taktzahl mit einfachen Maßnahmen zu steigern.

Die Kollisionsoptimierung ist ein sehr effektives Mittel zur Bewegungsoptimierung. Kollisionsoptimierung bedeutet dynamische Optimierung mit Kollisionskontrolle. Parallel zur Optimierung des Bewegungsdiagramms wird der daraus entstehende Bewegungsablauf grafisch simuliert. Man versucht, die Kollisionen im Bewegungsablauf so knapp wie zulässig zu vermeiden, und dabei die dynamischen Belastungen gleichmäßig auf alle Einzelantriebe zu verteilen. Letztlich sollten alle Einzelantriebe die gleiche maximale Taktzahl erreichen.

Die Kollisionsoptimierung ist sehr wirkungsvoll bei gleichzeitig niedrigem Aufwand. Sie hat für den Maschinenentwickler quasi ein optimales Preis-Leistungs-Verhältnis. In praktischen Anwendungen haben wir oft mehr als 30 % Taktzahlsteigerung erreicht durch Kollisionsoptimierung. Mit Kollisionsoptimierung haben wir viel und langjährige Erfahrung. Hier finden Sie ein Beispiel von 1996.

Bewegungspläne können mit unserer Software OPTIMUS MOTUS parametrisch aufgebaut werden, und die Parameter können mit numerischen Verfahren auf beliebige Zielfunktionen hin numerisch optimiert werden. Das ist die ultimative Art der Bewegungsoptimierung.

Die Bewegung im folgenden Bild wurde nach einem speziellen Verfahren numerisch optimiert, um mit minimalen Beschleunigungen den vorgegebenen Toleranzkanal einzuhalten.

Sieht ein bißchen so aus wie die Fahrlinie eines Rennfahrers, der die Kurven schneidet, oder?

Bewegungsdesign ist ein ganzheitliches Vorgehen zur dynamisch günstigen Gestaltung von Bewegungsdiagrammen.

Ziel ist die optimale Ausnutzung der Mechanismen und der Antriebe, um möglichst hohe Performance zu erreichen.

zum Start der Seite

Bereichserweiterung:

Die Bereichserweiterung ist eine Technik zur Verminderung der dynamischen Belastungen in Kurven- und Servoantrieben innerhalb von Bewegungsabschnitten. Sie wird auch Hubzeitverlängerung genannt.

Im Allgemeinen wird die Bereichserweiterung bei Bewegungsabschnitten verwendet, die von einer Rast oder einer Umkehr in eine andere Rast bzw. Umkehr verlaufen. Sie läßt sich aber auf allgemeine Bewegungsabschnitte erweitern.

Bei der Bereichserweiterung nutzt man aus, daß die Werte der Wegfunktion an den Rändern eines ruckfreien Bewegungsabschnitts sich nur langsam mit dem Taktwinkel aufbauen, daß also relativ viel Zeit vergeht, bis sich ein bestimmter Weg aufbaut. Zweitens nutzt man aus, daß die Weg-Endlagen bei Bewegungsabschnitten nur mit einer bestimmten Genauigkeit eingehalten werden müssen, nicht aber bis auf die achte Nachkommastelle.

Vorgehensweise bei symmetrischen Bewegungsgesetzen:

1. Bestimmen des tatsächlich genutzten Taktwinkelbereichs phi_original_nutz im Bewegungsabschnitt der ursprünglichen Länge phi_original. (siehe Skizze)

2. Berechnung der neuen Nutzlänge: phi_neu_gesamt = phi_original² / phi_original_nutz

Bei unsymmetrischen Bewegungsgesetzabschnitten sind die Taktwinkelverschiebungen der linken und der rechten Grenzlage unterschiedlich!

Beispiel:

In einem Bewegungsabschnitt über 100 mm Hub bei 120 Grad Taktwinkel wird das Bewegungsgesetz “Modifizierte Sinuslinie” eingesetzt. Die Endlagen müssen aber nicht genau mit 0 mm Toleranz, sondern nur mit 0.1 mm Toleranz eingehalten werden.

Aus der Hub-Tabelle für den Bewegungsabschnitt geht hervor, daß 0.1 mm Weg nach etwa 5.3 Grad Taktwinkel erreicht werden. 99.9 mm Weg werden nach etwa 114.7 Grad Taktwinkel erreicht:

phi [Grad]   s [mm]

   0.0     0.000
   0.5     0.000
   1.0     0.001
   1.5     0.002
   2.0     0.005
   2.5     0.010
   3.0     0.018
   3.5     0.029
   4.0     0.043
   4.5     0.060
   5.0     0.083
   5.5     0.110
   6.0     0.142
   6.5     0.180
   7.0     0.224
...
 113.0    99.776
 113.5    99.820
 114.0    99.858
 114.5    99.890
 115.0    99.917
 115.5    99.940
...
 

Zwischen 0.1 mm Weg und 99.9 mm Weg (also zwischen den beiden tolerierten Grenzlagen) liegt ein Taktwinkel von 109.4 Grad (statt theoretisch 120 Grad bei Nulltoleranz). Der gesamte Bewegungsabschnitt von bisher 120 Grad Länge kann nun zeitlich so gedehnt werden, daß aus den 109.4 Grad Taktwinkel 120 Grad Taktwinkel werden. Der Skalierungsfaktor auf der Zeitachse phi beträgt also 120/109.4.

Der erweiterte Taktwinkelbereich für den Bewegungsabschnitt beträgt damit

phi_neu_gesamt = 120 • (120 / 109.4) = 131.6 Grad

Durch Ausnutzung der für praktische Belange meist kleinen Toleranz von 0.1 mm reduzieent sich die maximale Geschwindigkeit in dem Abschnitt um 9 %, die Beschleunigung und die dynamischen Kräfte um 17 % und das dynamische Antriebsmoment um 24 %!

zurück zum Start der Seite

HS-Profile

HS-Profile bezeichnen eine spezielle Art der Bewegungsgestaltung für periodisch arbeitende Mechanismen mit Kurven oder Servoantrieben. „HS“ steht für „Harmonische Synthese“ und bedeutet, dass Bewegungen als Fourierreihe, durch Überlagerung von Sinusfunktionen mit jeweiligen Amplituden und Phasenverschiebungen gestaltet werden. HS-Profile werden besonders für schnell laufende „High-Speed“-Mechanismen verwendet, die für Eigenschwingungen anfällig sind.

HS-Profile beziehen sich auf den gesamten Bewegungszyklus der periodisch arbeitenden Maschine, nicht auf einen einzelnen Bewegungsabschnitt.

Bei der Berechnung von Kurven wird die gewünschte Bewegung meist am Abtrieb vorgegeben. Die Kurvenprofile werden daraus rein kinematisch berechnet, ohne Berücksichtigung von Elastizitäten.

Mechanismen sind aber in Wirklichkeit immer elastisch. Der kinematischen Grundbewegung sind deshalb immer Eigenschwingungen überlagert. Oft ändern sich die Eigenfrequenzen während eines Umlaufs nur wenig und können als konstant betrachtet werden. Bei entsprechend hoher Taktzahl bzw. hohem

Abstimmungsverhältnis η = Taktzahl/Eigenfrequenz

werden die überlagerten Eigenschwingungen so groß, dass die Funktion des Mechanismus beeinträchtigt wird.

Es ist nicht möglich, eine feste Grenze für das zulässige Abstimmungsverhältnis anzugeben, bis zu der die überlagerten Eigenschwingungen unbedenklich sind, weil die Anregung der Eigenschwingungen sehr von der Bewegungsgestaltung abhängt und die Genauigkeitsanforderungen unterschiedlich sind.

Man kann die überlagerten Eigenschwingungen aber grob mit Hilfe von Einmassenschwingermodellen abschätzen oder genauer durch Simulation mit MKS-Programmen ermitteln.

Ziel beim Einsatz eines HS-Profils ist, die dynamischen Abweichungen von der gewollten Bewegung bei Betriebsdrehzahl zu minimieren. Die Idee besteht darin, den Mechanismus im Bereich der Eigenfrequenzen möglichst wenig anzuregen, da eine Anregung in diesem Bereich die kinematisch vorgegebene Bewegung besonders stark verfälscht. Deshalb wird die Bewegung aus wenigen Harmonischen zusammengesetzt, deren höchste Frequenz deutlich unter der niedrigsten Eigenfrequenz des Mechanismus bleibt. Die k-te Harmonische ist dabei eine Sinusfunktion mit der Frequenz k ● Taktzahl.

Die resultierende Bewegung am Abtrieb setzt sich aus der anregenden Bewegung der Kurve und den überlagerten Eigenschwingungen zusammen. Diese resultierende Bewegung soll bei Betriebsdrehzahl so nah wie möglich an der für den Abtrieb gewünschten Bewegung liegen.

Folgende zwei Ansätze sind bei der Anwendung von HS-Profilen besonders bedeutsam:

Ansatz 1:

Vorgabe eines Bewegungsdiagramms und Verwendung der ersten N Harmonischen aus der Fourieranalyse eines Bewegungsdiagramms, das in der Regel abschnittsweise definiert wird:

Die Anzahl N zu berücksichtigender Harmonischer kann so gewählt werden, dass die Abweichung der resultierenden Bewegung am Abtrieb von der gewünschten Bewegung minimal wird.

Werden zu wenigen Harmonischen verwendet, ist die kinematische Abweichung durch das HS-Profil sehr groß, so dass der Mechanismus schon bei kleiner Taktzahl nicht richtig funktioniert.

Bei zu vielen Harmonischen werden schon die Eigenschwingungen angefacht.

Ansatz 2:

Vorgabe von Toleranzschläuchen für die resultierende Bewegung am Abtrieb und Ermittlung des HS-Profils mit einem numerischen Optimierungsalgorithmus.

Bei dieser Technik gibt man Toleranzkanäle vor, die sowohl von der kinematischen Bewegungsvorgabe (der Anregung) als auch von der auf Basis eines Einmassenschwinger-Modells abgeschätzten Reaktion am Abtrieb eingehalten werden sollen.

Ein speziell konzipiertes numerisches Verfahren sucht ein HS-Profil mit einer vorgegebenen Zahl von Harmonischen, das diese Toleranzkanäle einhält und außerdem eine lineare Zielfunktion optimiert, beispielsweise die Summe der Amplituden der Harmonischen.

Dieses sehr leistungsfähige Verfahren kommt mit sehr wenigen Harmonischen aus, um die Toleranzkanäle einzuhalten, so dass die erzeugten Bewegungsprofile erst bei hoher Taktzahl Eigenschwingungen in störender Größe anregen.

Beide Ansätze sind in der Mechanismensoftware OPTIMUS MOTUS (R) implementiert.

zurück zum Start der Seite

Kubische Splines

Die kubische Spline-Interpolation gehört eigentlich nicht zu den Methoden, mit denen Bewegungen “designt”, also gestaltet werden. Sie ist aber von großer Bedeutung, wenn Bewegungen ruckfrei abgebildet werden sollen, die über Tabellen mit vielen Stützpunkten definiert sind.

Vorgabe:

zunächst n+1 Stützpunkte X_i,Y_i mit i = 1..n+1

Ziel:

Berechnung einer Folge von n Parabeln F_i(x) dritter Ordnung, so dass Weg, Geschwindigkeit und Beschleunigung über den gesamten Bereich X₁ .. X_n+1 stetig sind.

Bedingungen:

F_i  (X_i  ) = Y_i
F_i  (X_i+1) = Y_i+1

für i = 1..n und

F_i' (X_i+1) = F_i+1' (X_i+1)
F_i''(X_i+1) = F_i+1''(X_i+1)

für i = 1..n-1
 

Insgesamt liegen also 4n - 2 Bedingungen vor, aber 4n Polynomkoeffizienten sind frei, für jedes der n Polynome dritter Ordnung 4 Koeffizienten.

Daher können zwei zusätzliche Bedingungen erfüllt werden, beispielsweise:

F₁'(X₁) = v0
F_n'(X_n+1) = v1

zur Vorgabe von Randgeschwindigkeiten v0 und v1 eines Bewegungsabschnitts oder

F₁'(X₁) = F_n'(X_n+1)
F₁''(X₁) = F_n''(X_n+1)

für die Ruckfreiheit bei periodische Funktionen.

Alle Interpolationsbedingungen zusammen ergeben ein lineares Gleichungssystem spezieller Ausprägung, das mit optimierten Algorithmen auch bei sehr vielen Stützpunkten schnell gelöst werden kann.

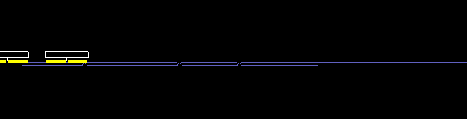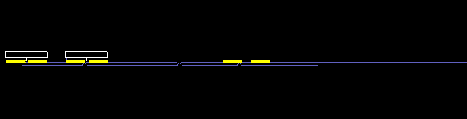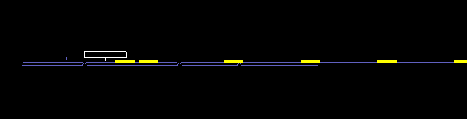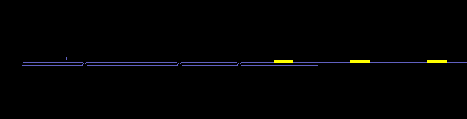
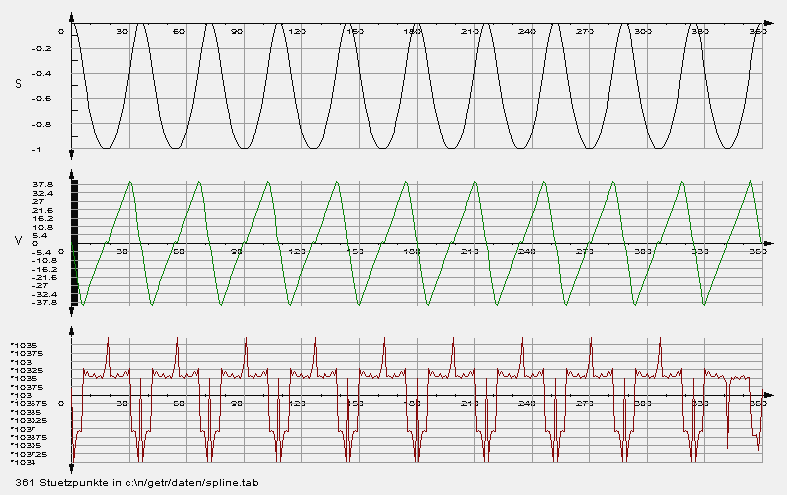
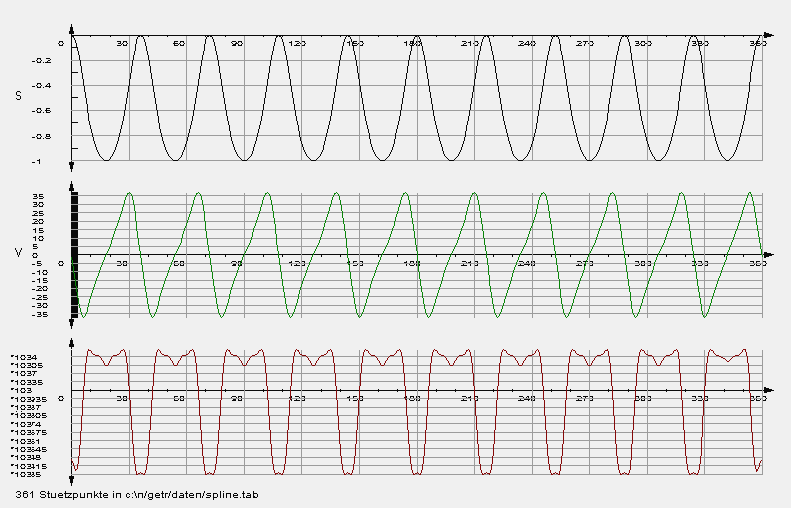
Typisch bei der Verwendung von Stützpunkttabellen bei Mechanismenberechnungen ist, dass die Original-Stützpunkte Meß- oder Rundungsfehler aufweisen, so dass die Ableitungen, speziell die Beschleunigungsverläufe, “verrauscht” aussehen. Dann ist es wichtig, die Stützpunkte im Rahmen definierbarer Toleranzen zu glätten, um sie für die weiteren Berechnungen überhaupt verwenden zu können.

Unsere Software OPTIMUS MOTUS bietet dazu geeignete Glättungsalgorithmen an.

Beispiel:

Weg-Zeit-Tabelle mit Geschwindigkeit (grün) und Beschleunigung (rot) aus einer NC-Datei (Rundung auf 3 Nachkommastellen):

... und nach der Glättung mit OPTIMUS MOTUS:

zurück zum Start der Seite

Gerne unterstützen wir Sie mit unserem Bewegungsdesign dabei, Ihre Maschinen schneller laufen zu lassen!

zur Startseite von Nolte NC-Kurventechnik GmbH

Start Fachberichte Mechanismen Kinematik Kurvengetriebe Schrittgetriebe Servo/SPS Fortbildung Service Kurvenberechnung Software Impressum Datenschutz
Beispiele Allgemeines Bewegungsgesetze Seminare Bereichserweiterung Kollisionsoptimierung Energieoptimierung HS-Profile Splines  

> zu unseren Kontaktdaten